开普勒三大定律的内容
1、开普勒第一定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
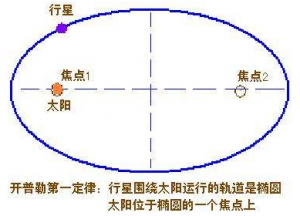
(开普勒第一定律)
2、开普勒第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等。
这个定律告诉我们,行星离太阳越近,运动的速度就越快,离太阳越远,运动的速度就越慢。
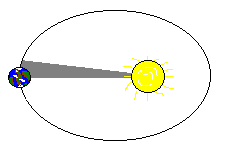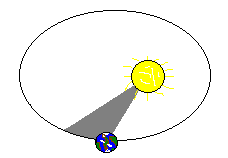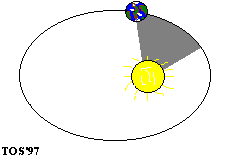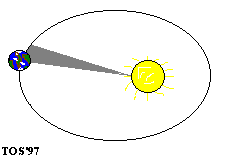
(开普勒第二定律)
3、开普勒第三定律:所有行星的轨道的半长轴的三次方和它的公转周期的二次方的比值都相等。即
![]() (a为长半轴;T为行星公转周期;k为常数,k与中心天体的质量有关)
(a为长半轴;T为行星公转周期;k为常数,k与中心天体的质量有关)
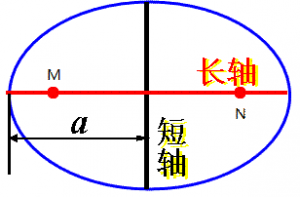
(开普勒第三定律)
开普勒三大定律的背景
开普勒的师父第谷是一位天才观测家,第谷出生在哥白尼去世后的三年,他把全部的时间都投入到行星运动的观测中,第谷所观测到的行星运动数据准确性比前人大大提高,这也为后来开普勒提出三定律做出条件保证。
在1600年,开普勒开始与第谷一起工作,但可惜的是,在它们一起工作18个月后,第谷去世,幸好第谷留下了它毕生所观测的行星运动数据,在谷布去世后,开普勒全身心的去整理第谷留下的数据,重重艰难险阻、与旧思想不断的碰撞(当时都认为行星绕太阳运动为匀速圆周运动),经过长达16年的时间,先后在1609年和1619年发表了行星运动的三个定律,也就是开普勒三大定律。
开普勒三大定律与万有引力定律
开普勒三大定律的提出是人们对地球以外行星运动认识的一次伟大飞跃,行星的运动居然是可以用公式预测的,那么复杂众多的数据居然可以归纳成几句简洁的话,这是科学的胜利,但开普勒却没有进一步思考,因为在开普勒第三定律中隐藏了万有引力定律。
开普勒三大定律的提出为牛顿推导出万有引力定律奠定了坚实的基础,在推导万有引力定律公式的过程中,必须要用到开普勒第二定律,在经过严格的数学证明和牛顿三大定律,最初推导出万有引力定律。
科学的发现就是这样,一代又一代科学家在前人的基础上,发现更重大的发现,难怪牛顿曾说过,“如果我比其他人看的更远些,那是因为我站在了巨人的肩膀上”。
万有引力定律推导公式是:根据开普勒三定律以及牛顿第三定律得出,F 向 为行星的向心力,F 引 为行星与太阳之间的吸引力。
具体如下:F 引=F 向=mw2r=mv2/r,
再由线速度与周期的关系得到:
F 引=m(2πr/T)2/r=4π2mr/T2
F 引=4π2mr/T2=4π2(r3/T2)m/r2
F 引=4π2km/r2,
所以可以得出结论:太阳对行星的引力跟行星的质量成正比,跟行星到太阳的距离的二次方成反比,
即:F∝m/r2。
牛顿根据牛顿第三定律大胆的猜想:既然太阳对行星的引力与行星的质量成正比,也应该与太阳的质量成正比,
F 引∝Mm/r2 写成等式:F 引=GMm/r2。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底