胡克还是英国皇家学会会长时,就曾请教过牛顿,问牛顿是否能通过“引力和距离平方成反比”,来推导行星椭圆运动规律,牛顿给胡克的回答是肯定的,但是并没有告诉胡克具体的推导过程。
牛顿大神利用自创的微积分,加上天才的头脑,推导行星椭圆轨道,简直就是易如反掌。
现在我们借助虚数的性质,把万有引力定律表示为矢量形式:
万有引力的发现历史,如何利用万有引力定律,推导行星椭圆轨道?
其中(-e^iθ)借助欧拉公式后,表示的就是单位大小的矢量因子,给出了万有引力的方向,同时与万有引力结合参与运算;至于负号,是因为θ=0时,万有引力方向指向原点;并利用牛二定律,得到加速度a。
然后,我们需要考察速度和加速度极坐标的微分形式:
然后两个加速度公式,得到微分方程:
求解该微分方程,就可以得到轨道方程的解:
该轨道方程,正是圆锥曲线的标准方程,其中e为偏心率!
(1)当e=0时,曲线为正圆;
(2)当0<e<1时,曲线为极点在下焦点的椭圆;
(3)当e=1时,曲线为开口向上的抛物线;
(4)当e>1时,曲线为极点在上焦点的双曲线;
至于偏心率实际为多少,取决于c1、C和GM,为大天体的引力场分布,和小物体的初始状态;sinθ=-1为近日点,sinθ=1为远日点。

 更多
更多

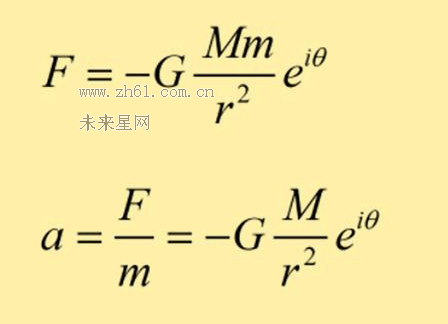



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底