第二宇宙速度（逃逸速度），即在地球附近而能离开地球的速度。第二宇宙速度从数学及物理学进行推导

1、热身
先看一个简单的问题: 地面上有一个质量为m的物体，以初速度V0竖直向上抛出，它能上升多高？

很明显，由于物体一直受到重力的作用，而且重力与其运动方向相反，重力是阻止物体向上运动的，重力对物体做负功，或者说，物体要克服重力做功：
W=mgh。

如果物体没有初速度，也就没有动能，是无法克服重力做功的，就是说，物体自己是不会跳起来的！必须别人推它获得初速度，也就有初动能：
 

在物体上升的过程中，物体由于要克服重力做功，本身的动能会越来越小，重力势能会越来越大，直到动能耗尽，Ek(top)=0，全部转化为势能为止，达到最高点，此时：
Ek=0
Ep=mgh （重力势能）
这个重力势能就是初始动能转化来的：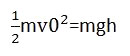
 

由此可以算出物体能达到的最大高度：
 
热身运动到此结束。

2、石头能不能扔出地球

回到上面的问题，物体在耗尽了动能之后，不会呆在最高点不动，马上就会掉下来！
为什么？
因为地球还对它有引力，也就是重力，会把它拉回地面，掉下来。不过你力气越大，扔得越高，直到看不见，不过要小心，它还是会砸下来的。
所以，我们用手是不能把一块石头扔上天的！

一定要把它扔上天，那就只好用火箭发射了。好在现在火箭越来越牛。
那么扔上天是什么意思？
就是不再掉下来，而且，再也不回地球了，去太阳系遨游，升级为太阳的人造卫星！

怎么可能？地球不是一直吸引它吗？当它动能耗尽，不是还会拉回来吗？
呵呵，不会。
因为，我们一直生活在地球，被重力吓怕了，其实，有一个重要的细节我们忽略了，那就是，重力并不是不变的，而是随着距离的增加猛减的。
这个，老牛同志（牛顿）早就说过了，重力不过是万有引力的一种而已：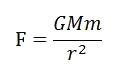
 
万有引力定律说明，随着距离的增加，引力按距离的平方减少，也就是说，如果我们能把石头扔到无穷远的话，地球的引力就无穷小了，可以不计。
所以，理论上，是可以扔出去的！
那么怎么计算要多大的速度呢？
那我们就要算出从地面到无穷远重力做了多少功。
那还不容易：
W=mgh∞
苦也！这个功是无穷大！那就意谓着要无穷大的速度，无穷大的力！

错！

3、远大的目光
既然是扔到天上去，我们就得站在天上看问题，再也不能在地球上思考了。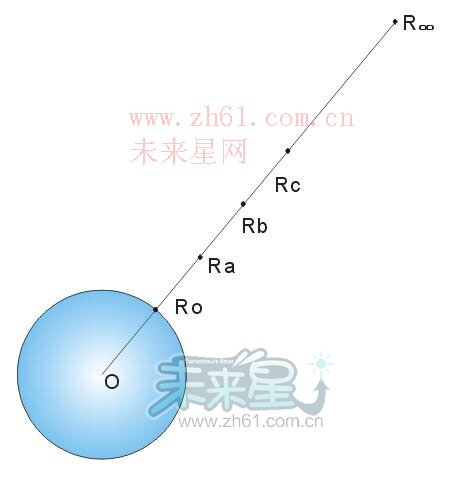
 
现在，我们站在天上看地球，就是个小球而已。没什么大不了的。
这时要注意了，我们站在地面思考问题时，总是把重力简化为G=mg，这个公式，只适合地面。

实际上它是随距离变化的，所以上面的公式中是不能用mg代表所有点的重力的。上面的o,a,b,c……每个点受到的重力都是不同的。
怎么办？
没办法，只好把距离切割为无数个小段了。

4、分割法
在地面取一点o，（参看上图）
它到地心的距离是Ro,就是地球的半径。
再依次取a点到地心距离为Ra
b点到地心距离为Rb
c点到地心距离为Rc
无穷远点到地心距离为R∞
要把石头扔到无穷远，那就要依次经过o-a,a-b,b-c……R(∞-1)-R∞
那么总的功应该是：
W总=Woa+Wab+Wbc+……+WR_(∞-1) R∞
可是Woa怎么算？
从o到a引力也是连续变化的。
不管它，先算出各点的引力再说：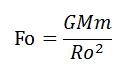
 
 
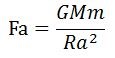
那取o点的呢还是a点呢，取谁另一方都不答应。
没办法，折中！取个大家都没意见的。
由于
 
那我们就用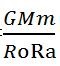 代表从o到a这一段的引力吧。
这样：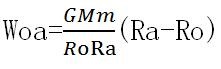
 
同理：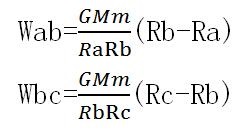
 

……以下省略无穷多个公式
 
变型为：
 
从地面到无穷远，重力做的总功为：
 

如果石头的初动能等于这个功，就能扔出地球了，大功告成！要是大于这个功，就飞得更远啰:
 

G为万有引力常数，M为地球质量，R0为地球半径，代入公式可得：
V0=11.2km/s
累死我了！
你要是学了微积分，我就没这么累了。一积分就出来。

5、微积分分析，基于机械能守恒进行计算
W=FR
微分：
dW=FdR
 

积分：