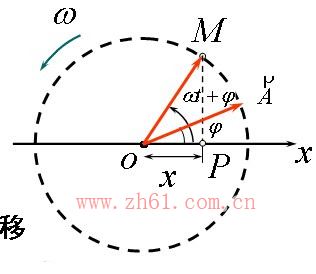
旋转矢量法是一种描述简谐振动较为直观的几何方法。从坐标原点O(平衡位置)画一矢量 ，使它的模等于谐振动的振幅A，并令t=0时A与x轴的夹角等于谐振动的初相位φ₀，然后使A以等于角频率ω的角速度在平面上绕O点作逆时针转动，这样作出的矢量称为旋转矢量。显然，旋转矢量 任一时刻在x轴上的投影x=Acos(ωt+φ₀)就描述了一个简谐振动。
当旋转矢量绕坐标原点旋转一周，表明简谐振动完成了一个周期的运动。任意时刻旋转矢量与x轴正向的夹角就是该时刻的相位。