单摆的概念
单摆是一种理想的物理模型,它由理想化的摆球和摆线组成。
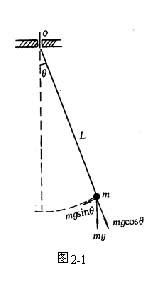
单摆是能够产生往复摆动的一种装置,将无重细杆或不可伸长的细柔绳一端悬于重力场内一定点,另一端固结一个重小球,就构成单摆。
单摆的周期公式
若小球只限于铅直平面内摆动,则为平面单摆,若小球摆动不限于铅直平面,则为球面单摆。
单摆运动近似的周期的公式:
![]()
其中L指摆长,g是当地重力加速度。
从公式中可看出,单摆周期与振幅和摆球质量无关。
受力角度分析,单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力,偏角越大,回复力越大,加速度(gsinθ )越大,在相等时间内走过的弧长也越大,所以周期与振幅、质量无关,只与摆长L和重力加速度g有关。
在有些振动系统中L不一定是绳长,g也不一定为9.8m/s² ,因此出现了等效摆长和等效重力加速度的问题。物理上有些问题与单摆类似,经过一些等效可以套用单摆的周期公式,这类问题称为“等效单摆”。等效单摆在生活中比较常见.除等效单摆外,单摆模型在其他问题中也有应用。
绕一个悬点来回摆动的物体,都称为摆,但其周期一般和物体的形状、大小及密度的分布有关。但若把尺寸很小的质块悬于一端固定的长度为 l且不能伸长的细绳上,把质块拉离平衡位置,使细绳和过悬点铅垂线所 成角度小于5°,放手后质块往复振动,可视为质点的振动,其周期 T只和l和当地的重力加速度g有关,即 而和质块的质量 、形状和振幅的大小都无关系,其运动状态可用简谐振动公式表示,称为单摆或数学摆。如果振动的角度大于 5°,则振动的周期将随振幅的增加而变大,就不成为单摆了。如摆球的尺寸相当大,绳的质量不能忽略,就成为复摆(物理摆),周期就和摆球的尺寸有关了。
利用单摆测当地重力加速度的实验
单摆只在最大摆角小于等于5°时,单摆的振动才可以近似看为为简谐振动。单摆的固有周期公式:
![]()
由该式可推导:
![]()
据此,我们只要通过实验方法测出摆长L和周期T,就可以通过计算得到当地的重力加速度。
我们还可以测量借助坐标图像来处理数据,得到g的数值。具体请参考高中物理网文章《单摆测重力加速度》
重力加速度的改变
重力加速度g的方向总是竖直向下的。在同一地区的同一高度,任何物体的重力加速度都是相同的。
重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时,g变化不大。而离地面高度较大时,重力加速度g数值显著减小,此时不能认为g为常数。
距离地面同一高度的重力加速度,也会随着纬度的升高而变大。由于重力是万有引力的一个分力,万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。
物体所处的地理位置纬度越高,圆周运动轨道半径越小,需要的向心力也越小,重力将随之增大,重力加速度也变大。
地理南北两极处的圆周运动轨道半径为0,需要的向心力也为0,重力等于万有引力,此时的重力加速度也达到最大。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底