力的合成与分解
力的合成与力的分解是研究力的两个最基本的方法。同时也是我们受力分析研究的一个基础。力的合成与分解其实是数学向量知识的实际应用之一。
几个力共同作用产生的的效果可以用一个力来代替,这个力就叫做那几个力的合力;而这几个力就是这个合力的分力。力的合成与分解互为逆运算,都符合平行四边形法则。
力的合成概念
求几个力的合力的过程,叫做力的合成。
力的分解概念
求一个的分力叫做力的分解。
力的平行四边形定则
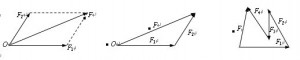 求两个互成角度的共点力的合力,可以用表示这两个力的线段为邻边作平行四边形,合力的大小和方向就可以用这个平行四边形的对角线表示出来。反之,求力的分解,步骤相反。平行四边形定则实质上是一种等效替换的方法。一个矢量(合矢量)的作用效果和另外几个矢量(分矢量)共同作用的效果相同,就可以用这一个矢量代替那几个矢量,也可以用那几个矢量代替这一个矢量,而不改变原来的作用效果。
求两个互成角度的共点力的合力,可以用表示这两个力的线段为邻边作平行四边形,合力的大小和方向就可以用这个平行四边形的对角线表示出来。反之,求力的分解,步骤相反。平行四边形定则实质上是一种等效替换的方法。一个矢量(合矢量)的作用效果和另外几个矢量(分矢量)共同作用的效果相同,就可以用这一个矢量代替那几个矢量,也可以用那几个矢量代替这一个矢量,而不改变原来的作用效果。
力的三角形定则
如果一个物体仅受三个力的作用而处于平衡状态,那么这三个力的矢量可以构成一个封闭的三角形,且首尾依次连接。如上面图像所示。
这一点,大家不妨去分析一个简单的受力图:一个重力为6N的物体被细线吊着,细线悬在天花板上,在一个水平的大小为8N的弹簧弹力作用下处于平衡态。
三角形定则可以推广到多个力的合成情况。只要将表示各个分力的有向线段首尾相接成一折线(与先后顺序无关),那么从第一个有向线段的箭尾到最后一个有向线段的箭头的有向线段就表示它们的合力F。由三角形定则还可以得到一个有用的推论:如果n个力首尾相接组成一个封闭多边形,则这n个力的合力为零。如图所示。
力的合成与分解做题注意事项
在分析同一个问题时,合矢量和分矢量不能同时使用。也就是说,在分析物理问题时,考虑了合矢量就不能再考虑分矢量;考虑了分矢量就不能再考虑合矢量。力的合成分解,一定要认真作图。在用平行四边形定则时,分矢量和合矢量要画成带箭头的实线,平行四边形的另外两个边必须画成虚线。各个矢量的大小和方向一定要画得合理。在应用正交分解时,两个分矢量和合矢量的夹角一定要分清哪个是大锐角,哪个是小锐角,不可随意将两个锐角都画成45º。(当题目规定为45º时除外);在一般不规定θ角度到底是多少,我们建议学生们画成30度进行分析。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底