简谐运动既是最基本也是最简单的一种机械振动。当某物体进行简谐运动时,物体所受的力跟位移成正比,并且力总是指向平衡位置。
基本信息
中文名称:简谐振动
别称:简谐运动
表达式:x=Ae^(-nt)sin(wt+θ)
应用学科:力学
目录
1基本介绍
2周期频率
3运动方程
4微分方程解法
5阻尼振动
6受迫振动
7弹簧振子
基本介绍
如果用F表示物体受到的回复力,用x表示小球对于平衡位置的位移,根据胡克定律,F和x成正比,它们之间的关系可用下式来表示:
F = - k x
式中的k是回复力与位移成正比的比例系数,不能与弹簧的劲度系数混淆;负号的意思是:回复力的方向总跟物体位移的方向相反。
根据牛顿第二定律,F=ma,当物体质量一定时,运动物体的加速度总跟物体所受合力的大小成正比,并且跟合力的方向相同。简谐运动系统的机械能守恒。
周期频率
一般简谐运动周期:T=2π√(m/k). 其中m为振子质量,k为振动系统的回复力系数。
对于单摆运动,其周期T=2π√(L/g) (π为圆周率 √为根号 ) 由此可推出g=(4π^2×L)/(T^2) 据此可利用实验求某地的重力加速度。
T与振幅(a<10度)和摆球质量无关。
当偏角a<10度时 sina≈a=弧(轨迹)/L(半径)≈x/L;F回=-mg/Lx
根据牛顿第二定律,F=ma,运动物体的加速度总跟物体所受的合力的大小成正比,并且跟合力的方向相同。
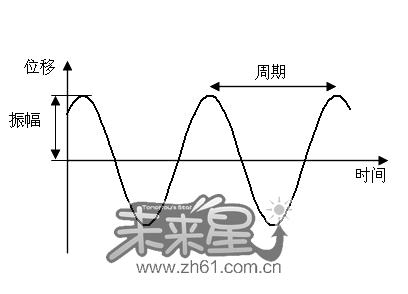
振幅、周期和频率
简谐运动的频率(或周期)跟振幅没有关系。
物体的振动频率本身的性质决定,所以又叫固有频率。
运动方程
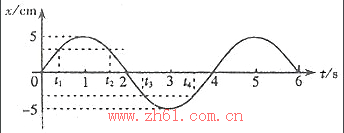
一个做匀速圆周运动的物体在一条直径上的投影所做的运动即为简谐运动:R是匀速圆周运动的半径,也是简谐运动的振幅;ω是匀速圆周运动的角速度,也叫做简谐运动的圆频率,ω=√(k/m);φ是t=0时匀速圆周运动的物体偏离该直径的角度(逆时针为正方向),叫做简谐运动的初相位。在t时刻,简谐运动的位移x=Rcos(ωt+φ),简谐运动的速度v=-ωRsin(ωt+φ),简谐运动的加速度a=-(ω^2)Rcos(ωt+φ),这三个式子叫做简谐运动的方程。
这个运动是假设在没有能量损失引至阻力的情况而发生。
做简谐运动的物体的加速度跟物体偏离平衡位置的位移大小成正比,方向与位移的方向相反,总指向平衡位置。
微分方程解法
方程:(d x)*(d x)/(d t*t)+kx/m=0
通解:x(t)=c1*cos(kt)+c2*sin(kt)
特解:x(t)=x0*cos(kt)+v0/k*sin(kt)
令:x0=Asinθ结论:Asin(kt+θ)
振幅为A,初相为θ,周期为T=2π/k,角频率为k。
其中k为系统的固有频率。
当物体到最低点时,v=f(x)取极值,速率取最大值,此时a=f'(x)=0。
当物体到最高点时,v=f(x)=0,速率取最大值,此时a=f'(x)在不同方向上最大。
简谐运动
振动过程中受到阻力的振动,振幅逐渐减小,直至振动停止。
振动方程:x=Ae^(-nt)sin(wt+θ).
受迫振动
在外界驱动力作用下的简谐振动,频率只与驱动力频率有关。
驱动力频率越接近固有频率,振幅越大。
驱动力频率与固有频率相等时,振幅随时间正比增大,发生共振。
受迫振动与共振:
⑴受迫振动:振动系统在周期性作用下的振动。稳定时,系统的振动频率等于策动力的频率,跟系统的固有频率无关。
⑵共振:当策动力的频率等于系统的固有频率时振幅最大称为共振。
弹簧振子
将一个有孔小球体与一个弹簧连在一起,将一个极为光滑的水平杆穿入小球体,使球体可以在水平杆上左右滑动,而球体与水平杆的摩擦力小得可以忽略不计。将弹簧的一端固定住,弹簧的整体质量要比球体质量小得多,这样弹簧本身质量也可以忽略不计。这个系统便是一个弹簧振子。
弹簧振子系统在平衡状态下,弹簧没有形变,振子(小球体)在平衡位置保持静止。若把振子拉过平衡位置,到达最大幅度,再松开,弹簧则会将振子向平衡位置收回。在收回的过程中,弹簧的势能转换为振子的动能,势能在降低的同时,动能在增加。当振子到达平衡位置时,振子所积累的动能又迫使振子越过平衡位置,继续向同样的方向移动。但因已越过弹簧振子系统的平衡位置,所以这时弹簧开始对振子向相反方向施加力。动能转作势能,动能降低,势能上升,直至到达离平衡位置最大幅度的距离。这时振子所有的动能被转化为势能,振子速度为零,停止运动。势能又迫使振子移回平衡位置,在移动过程中,势能转为动能,因而再次越过平衡位置,重复这个过程。在没有任何其他力影响的完美的条件下,这个弹簧振子系统会在两个最大幅度点间不停地做往返运动。 弹簧振子的固有周期和固有频率与弹簧劲度系数和振子质量有关,与振幅大小无关。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底