在万有引力作用下双星的运动
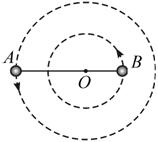
宇宙中往往会有相距较近,质量可以相比的两颗星球,它们离其它星球都较远,因此其它星球对它们的万有引力可以忽略不计。在这种情况下,它们将各自围绕它们连线上的某一固定点做同周期的匀速圆周运动。在天文学中,我们把这种运动模式的星体结构叫做双星。
设A、B双星运动的半径分别为r1与r2,则两者的距离为r=r1+r2;
其角速度是相等的w1=w2,周期也相等,都为T;
分别对m1与m2进行分析,我们可以根据万有引力提供向心力得到下述方程:
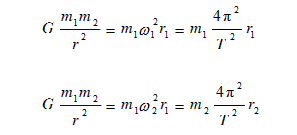
在万有引力作用下双星的运动特点总结
由于双星和该固定点总保持三点共线,所以在相同时间内转过的角度必相等,即双星做匀速圆周运动的角速度必相等,因此周期也必然相同。
由于每颗星的向心力都是由双星间相互作用的万有引力提供的,因此大小必然相等,由F引=mvω,得 ,因此,即固定点离质量大的星较近。
由于角速度相同,还可推出线速度大小跟质量成反比。
在解题的运算过程中需要注意:万有引力定律表达式中的r表示双星间的距离,而向心力表达式中的r表示它们各自做圆周运动的半径,两者是不一样的,因此在具体的问题中要具体对待,千万不可混淆。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底