傅科摆(Foucault pendulum)指仅受引力和吊线张力作用而在惯性空间固定平面内运动的摆。为了证明地球在自转,法国物理学家傅科(1819—1868)于1851年做了一次成功的摆动实验,从而有力地证明了地球是在自转,傅科摆由此而得名!
基本信息
中文名称:傅科摆
外文名称:Foucault pendulum
诞生于:法国巴黎先贤祠
分布于:北京天文馆 等地

基本概述
为了证明地球在自转,法国物理学家傅科(1819-1868)于1851年做了一次成功的摆动实验,傅科摆由此而得名。
实验在法国巴黎先贤祠最高的圆顶下方进行,摆长67米,摆锤重28公斤,悬挂点经过特殊设计使摩擦减少到最低限度。这种摆惯性和动量大,因而基本不受地球自转影响而自行摆动,并且摆动时间很长。摆动过程中,摆动平面沿顺时针方向缓缓转动,摆动方向不断变化。
傅科摆放置的位置不同,摆动情况也不同。在北半球时,摆动平面顺时针转动;在南半球时,摆动平面逆时针转动。而且纬度越高,转动速度越快,在赤道上的摆几乎不转动,在两极极点旋转一周的周期则为一恒星日(23小时56分4秒),简单计算中可视为24小时。傅科摆摆动平面偏转的角度可用公式θ°=15°tsinφ来求,单位是度。式中φ代表当地地理纬度,t为偏转所用的时间,用小时作单位,因为地球自转角速度1小时等于15°,所以,为了换算,公式中乘以15°。
悬挂方法
摆的运动超然于地球的自转,但我们要悬挂摆的支架也不参与地球的自转。傅科采取了一种装置——万向节,从而使摆动平面超然于地球的自转。
自转惯性
傅科摆为什么能够演示出地球自转呢?简单的说,因为惯性。
通常,我们说"地球具有自转"的时候,我们并没有明确出它到底相对于什么自转。这是一个非常重要的问题,如果没有参照物,谈论运动是不可想象的。我们没有办法在空间中打上一根钉子作为绝对的参照物,因此,我们只能依靠较远的、看起来似乎是静止的天体作为参照物。事实上,那些天体也绝不是"空间中的钉子",只不过因为它们实在太遥远了,我们不妨--事实上恐怕也是唯一的选择--把它们作为参照物。
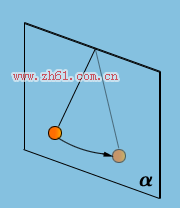 摆是一种很有趣的装置。给摆一个恰当的起始作用,它就会一直沿着某一方向,或者说某一平面运动。如果摆的摆角小于5°的话,(高中物理书允许在10°之内)摆锤甚至可以被视为做一维运动的谐振子。
摆是一种很有趣的装置。给摆一个恰当的起始作用,它就会一直沿着某一方向,或者说某一平面运动。如果摆的摆角小于5°的话,(高中物理书允许在10°之内)摆锤甚至可以被视为做一维运动的谐振子。
考虑一种简单的情况,假如把傅科摆放置在北极点上,那么会发生什么情况呢?很显然,地球在自转--相对于遥远的恒星自转。同样,由于惯性,傅科摆的摆锤相对于遥远恒星的运动方向(平面)是不变的。
你可以想象,有三颗遥远的恒星确定了一个平面,而傅科摆恰好在这个平面内运动。由于惯性,当地球以及用来吊起摆锤的架子转动的时候,摆锤仍然在那个平面内运动。
当你站在傅科摆附近的地球表面上,你会发现摆动的平面正在缓缓转动,它转动的速度大约是钟表时针转动速度的一半,也就是说,每小时傅科摆都会顺时针转过15度。摆在同一平面内运动,这里所说的平面是由远方的恒星确定的。
如果把傅科摆放置赤道上呢?那样的话,我们将观察不到任何转动。把摆锤的运动看做一维谐振(单摆),由于它的运动方向与地轴平行,而地轴相对遥远的恒星是静止的,所以我们观测不到傅科摆相对地面的转动。
在把傅科摆移回巴黎。摆锤的运动可以分解为沿地轴方向的和与之垂直方向上的两个分运动。后者会产生相对地面的旋转(正如北极的傅科摆)。这两个分运动合成的结果是,从地面上的人看来,傅科摆以某种角速度缓慢的旋转--介于傅科摆在北极和赤道的角速度之间。(也可以从科里奥利力的角度解释,得出的结论是一样的)如果在北极的观测到傅科摆旋转一周的时间是A(A=24h),那么在任意纬度γ上,傅科摆旋转一周所需的时间是A/sinγ。对于巴黎,这个数字是31.8小时。
傅科巧手
傅科摆实验非常简单地演示了地球自转现象,因此傅科获得了荣誉骑士五级勋章。
傅科使用了如此巨大的摆是有道理的。由于地球转动的比较缓慢(相对摆的周期而言),需要一个比较长的摆线才能显示出轨迹的差异。又因为空气阻力的影响,这个系统必须拥有足够的机械能(一旦摆开始运动,就不能给它增加能量)。所以傅科选择了一个28千克的铁球作为摆锤。此外,悬挂摆线的地方必须允许摆线在任意方向运动。傅科正是因为做到了这三点,才能成功地演示出地球的自转现象。

 更多
更多

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底