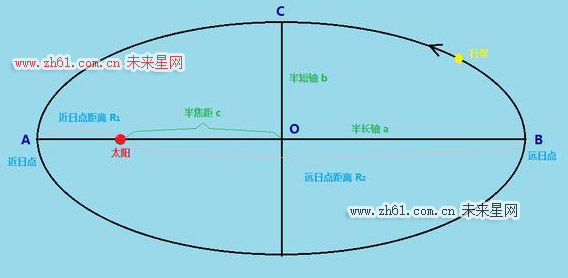
假如某行星围绕太阳作椭圆运动,太阳质量为M,行星近日点和远日点距离为R1和R2,那么行星围绕太阳公转运动的所有基本特征都可以确定,例如:
1)可确定公转轨道的椭圆方程:
2) 可确定近日点和远日点的速度:
(其中G为万有引力常量), 并且可确定公转轨道上任意点的速度及沿轨道运行的速度曲线,该曲线在近日点速度达到最大值V1,在远日点速度达到最小值V2
3) 可导出行星和太阳的连线在相同时间内扫过的面积相同(开普勒第二定律),
4) 可导出行星的公转周期:
5) 可导出公转周期的平方与半长轴的立方成正比(开普勒第三定律)
6)上述特征与行星本身的质量或体积大小无关。
以上特征或结论的详细推导在下一篇给出,有兴趣的读者可自行推导看看。这里以行星地球为例,验证一下地球围绕太阳公转的周期是否为365天:
实际上,地球的公转周期为365.25天(每四年闰一天,即公历年份可被4整除时,当年2月份的天数由28天增到29天)。

 更多
更多





 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底