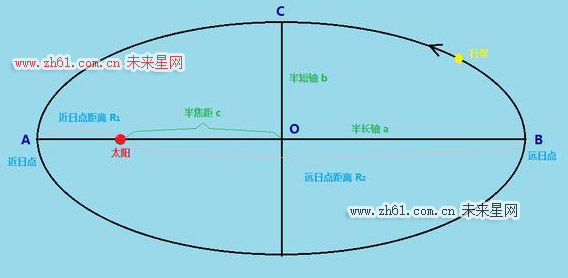
假如某行星围绕太阳作椭圆运动,太阳质量为M,行星近日点和远日点距离为R1和R2,那么行星围绕太阳公转运动的所有基本特征都可以确定,例如:
可确定公转轨道的椭圆方程:
我们先来推导椭圆的极坐标方程。
把极点选在椭圆的一个焦点上,让极轴沿着椭圆的长轴指向远离另一焦点的方向,如图
按照定义,椭圆是到两焦点的距离之和等于常数(设这常数为2a)的点的轨迹。椭圆的方程应为
(这里设两焦点间的距离为2c)
在上一方程中,先把左边的第一项r移到右边,再取两边的平方消去根号,我们得到
由此又可得到
这里
这样我们就得到了椭圆的极坐标方程
采用极坐标
这里M是太阳的质量,m是行星的质量,G是万有引力常数。行星的运动方程可以写成
这里K=GMm。后一方程两边乘以r得
或
这说明面积速度等于常数
再来考察方程
记u=1/r,则从
可得
我们有
方程(1)化成
即
这是一个二阶常系数线性微分方程。容易看出它的一个特解是  。于是,这个方程的一般解为
。于是,这个方程的一般解为
这式又可写成
其中
于是有
这里
我们得到了圆锥曲线的一般方程
因为旋转中的行星不会跑到无穷远去,它的轨道应该是一个椭圆。
该轨道方程,正是圆锥曲线的标准方程,其中e为偏心率!
(1)当e=0时,曲线为正圆;
(2)当0<e<1时,曲线为极点在下焦点的椭圆;
(3)当e=1时,曲线为开口向上的抛物线;
(4)当e>1时,曲线为极点在上焦点的双曲线;
至于偏心率实际为多少,取决于c1、C和GM,为大天体的引力场分布,和小物体的初始状态;sinθ=-1为近日点,sinθ=1为远日点。

 更多
更多




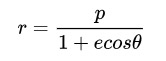

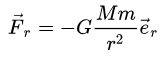
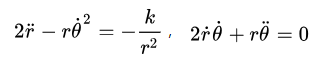
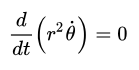
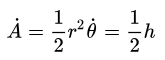

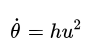
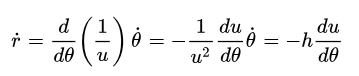
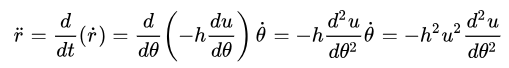

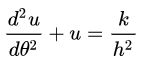
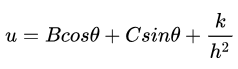

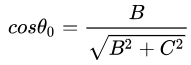
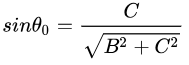
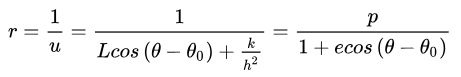

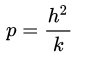
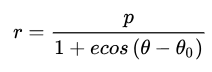
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底