编者说明:因文章内含有数学公式无法正常上传,故包含公式的部分内容改为截图的方式分享,以保证格式的正确性。对读者造成不便敬请海涵。
本文采用微积分的方法来推导球体的体积公式。
式中:v—球体体积,R—球体半径。
本文根据不同的细分方法分享三种不同的分析计算方法分别来推导求证。
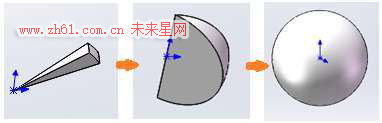
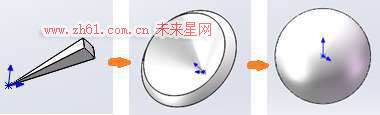
方法一,将球体按类似于切西瓜的方法进行切分,形象地称之为切西瓜细分法。

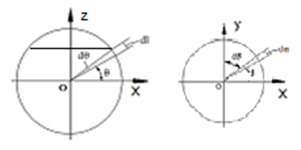

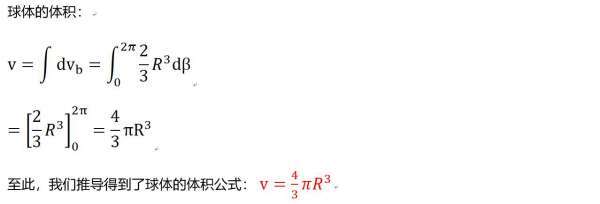
【说明】此方法的计算思路可以形象描述为:先计算西瓜块的体积,再算出一瓣西瓜的体积,最后算出整个西瓜的体积。如图所示:
我们也可以采用另一种积分思路,先计算出西瓜块的体积,再算出由西瓜块沿中心绕一周形成的西瓜环的体积,最后再算出整个西瓜的体积。
积分过程表达式如下:


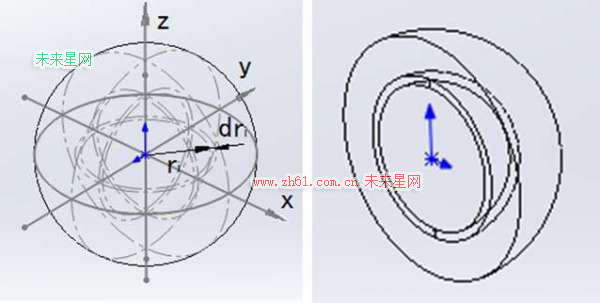
方法二:我们将球体沿轴向切分成无数个球壳,这种方法我们简称为球壳法。
如图所示,我们在球体内取一半径为r,厚度为dr 的球壳。


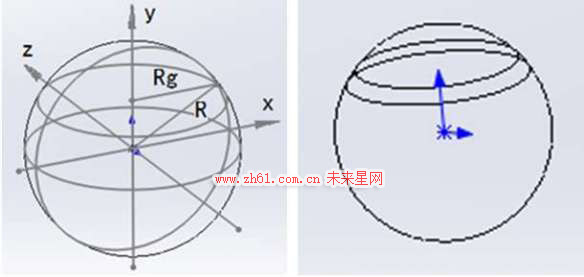
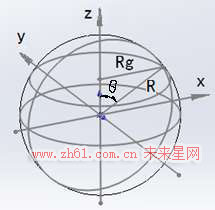
方法三:我们将球体切分成片,我们简称为切片法。

同样的细分方法还可以采用如下计算方式。
同样采用微积分的分析计算方式,可以选择不同的细分方式进行计算推导。也可以采用解析几何方式来分析计算。机械设计人当然要发挥自己空间想象力的优势选择几何细分的方式,可以简化复杂的计算过程。
声明:本文为《机械工程文萃》原创文章,如有雷同之处,不是巧合,是因为错误的方式有很多,正确的方法就那么几个,而且都是规定套路。

 更多
更多
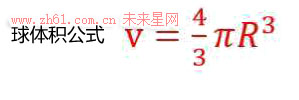



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底