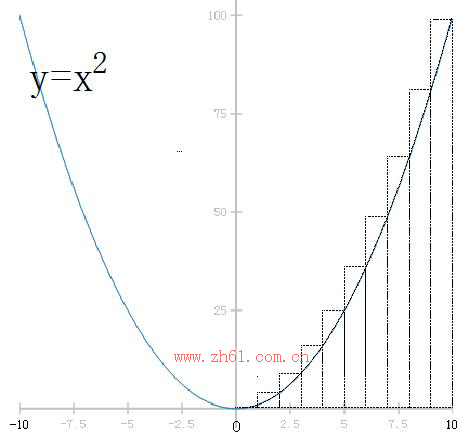
怎样求曲线x²和直线x=0、x=10、x轴围成的面积?
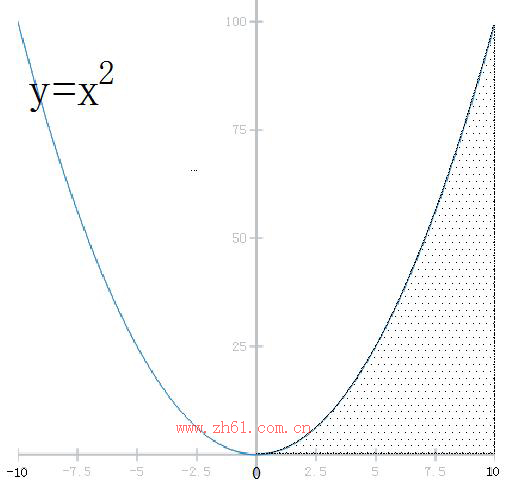
1 近似、暴力的方法:先分割、后求和
就是把不规则的图形分割为n个小的规则(梯形或矩形)的图形,计算n个小的规则的图形的面积,累加起来去近似整体的面积。
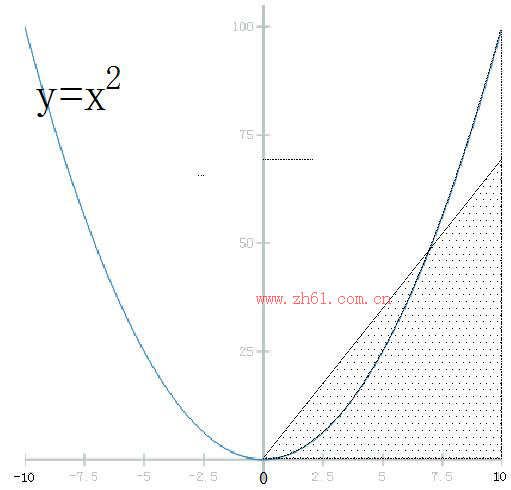
如果是这样的一块田地,测量人员要去测量的话,他们会怎样做呢?一般会通过一个三角形去近似。会量一个底为10,高为70左右的一个三角形,面积大概是350左右。
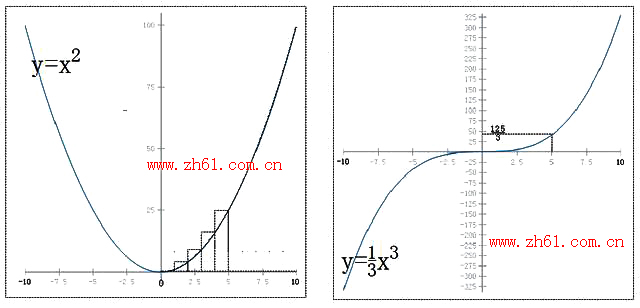
如果将区间[0,10]分成10个小区间,每个小区间的长度dx为1,在每个小区间[ti,tj]取点ξi(等于ti+0.5),每个dy=(ti+0.5)²,则将整个面积划分为10个长方形:
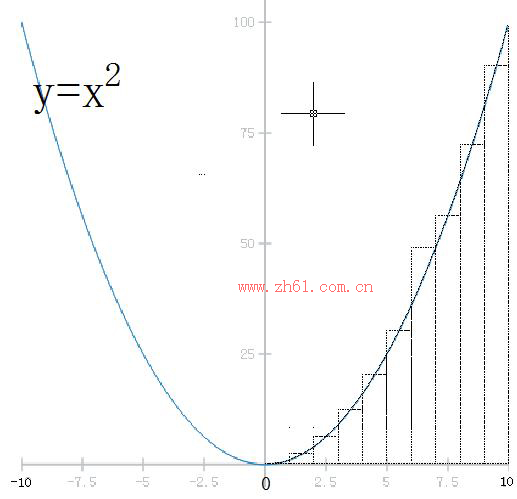
小区间求和的Σ的形式就是:
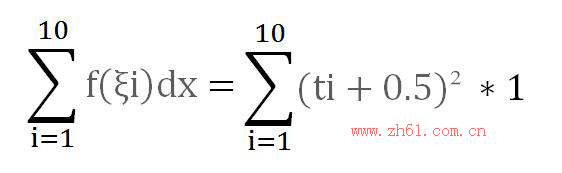
=0.5²+1.5²+2.5²+3.5²+4.5²+5.5²+6.5²+7.5²+8.5²+9.5²=332.5
2 极限或无穷的方法
引用极限或无穷的概念,如果上述的dx→0(n→∞),ξi取每个小区间的右端点:
有

当n→∞,上述=1000/3
3 定积分的方法
也可以用定积分的形式表示:
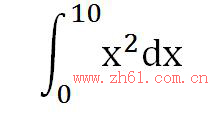
dx表示自变量在区间[0,10]的微分,x²dx表示整个面积的微分,符号∫是英文“sum'首字母“s”的拉长,表示面积微分的累加。
下面我们就一般情形来讨论定积分的近似计算问题。
若函数f(x)在区间[a,b]上连续,则下式定积分存在。

我们将区间[a,b]分成n个长度相等的小区间
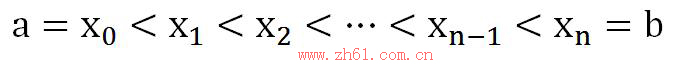
每个小区间的长度均为dx=(b-a)/n,每个小区间任取ξi,则有
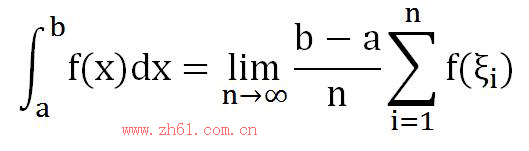
(上限无穷分割或定积分的方法不一定能求出极限值。)
4 由定积分变上限积分的面积函数
上面的定积分所计算出的都是一个特定的值(注意“定”这个字),不是一般的函数关系表达式。我们需要研究一般规律的函数关系表达式(不包含符号∫,这样就可以不是每次都用极限的方法而用代入的方法可以直接求出)。能不能找到一个关于x的面积函数,也就是曲线x²和直线x取任意值、x轴围成的面积函数,给出x的值,即可求出面积。
这样的面积函数的积分表达式可以表示为:
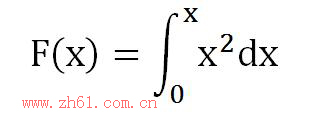
面积函数F(x)如何用没有∫符号的表达式表示?可以考虑的思路是,F(x)肯定与曲线函数x²有相关关系。
我们可以考虑x²曲线以外的一般情形y=f(t),面积函数为A(x),如下图:
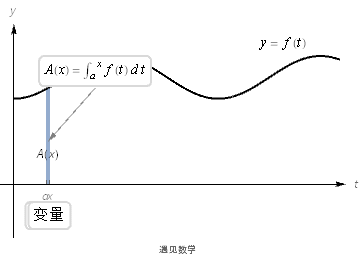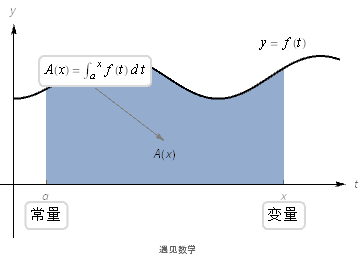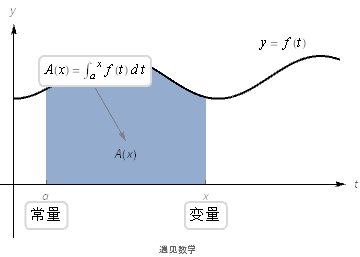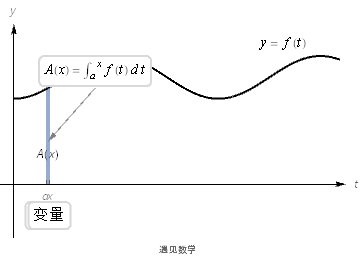
关键在于找出F(x)或A(x)的一般表达式,这个表达式是积分表达式的替代,从积分表达式可以看出,与面积微分f(t)dx或f(x)dx肯定有关系,是什么关系呢?
5 由变上限积分的面积函数到一般表达式的面积函数
当积分的上限为x,在此基础上,做自变量x和面积函数的微分,自变量x增加一个极小值h(dt):
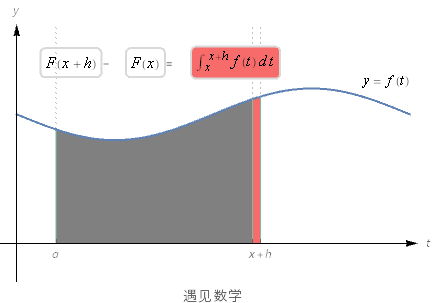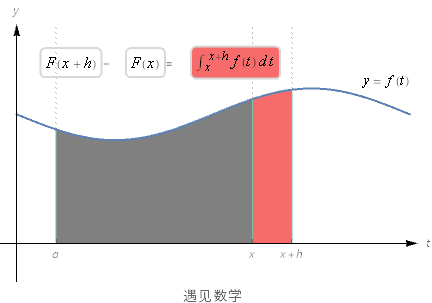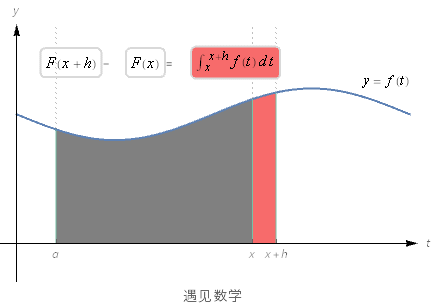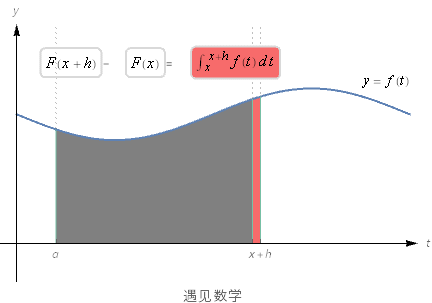
上图淡红色的阴影部分, 当 h 很小的时候几乎为小竖条, 所以可以用计算长方形面积的方法来估算该竖条的面积, 它的底从x 到x+h, 高从0 到f(x), 所以面积是 h*f(t) , 也就是:
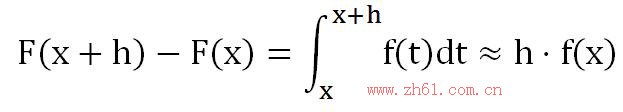
表达式h·f(x)就是面积函数F(x)的微分,函数的微分/自变量的微分称为微商,也称为导函数或导数,用F‘(x)表示。导数的形式在一定情形比微分的形式更简洁,微分也可以由导数迂回求得,如上式可有如下推导:
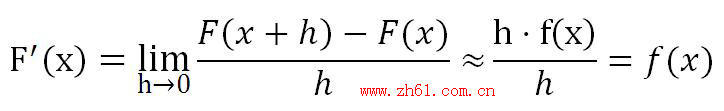
由此可见,曲线函数f(x)的反导数就是面积函数F(x),这就是微积分的基本定理。
上述黑色部分的面积可以表示为:F(x)-F(a),这就是微积分的基本公式。
函数的导数是一个函数的因变量相对于自变量变化的快慢,即“变化率”。可以用来求函数的最值、曲线在某一点的切线的斜率、变速运动的瞬时速度。
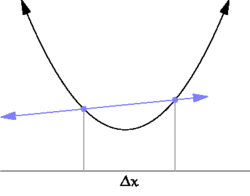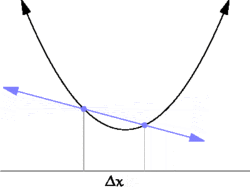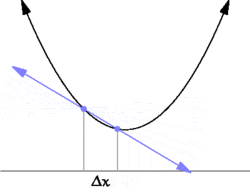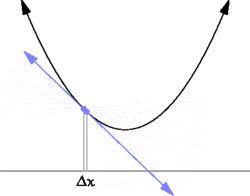
导数中引入了无穷小与极限的概念,但近似的表达式中却可以去掉无穷小与极限的符号,让表达式变得更简洁,如:
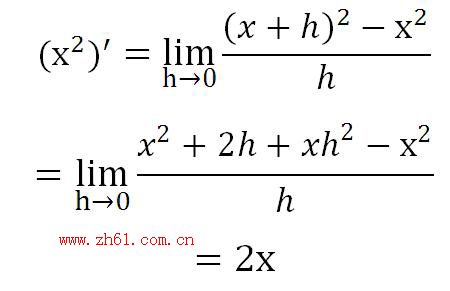
类似的
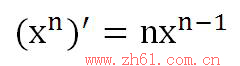
再回到下式:
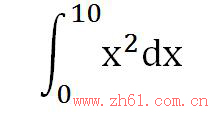
x²的反导数为1/3x³,所以上述所需求出的面积为:F(10)-F(0)=1000/3。
当然如果想求曲线x²和直线x=5、x=10、x轴围成的面积:F(10)-F(5)=1000/3-125/3=875/3=291.6。
6 从变速直线运动中路程函数与速度函数再看导数与积分的关系
设物体沿一直线做变速运动,在时间t时,其路程函数为s(t),速度函数为v(t),则在时间段[T1,T2]内,由定积分定义可知,物体经过的路程为
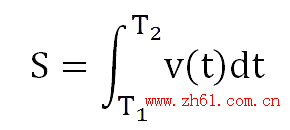
另一方面,S也可用路程函数s(t)的增量ΔS=S(T2)-S(T1)来表示,从而有关系式
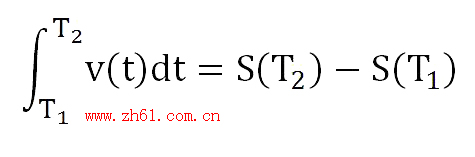
由于S‘(t)=v(t),即路程函数是速度函数v(t)的反导数,定积分由无限求和变成了求差。
如v(t)=t(8-t)
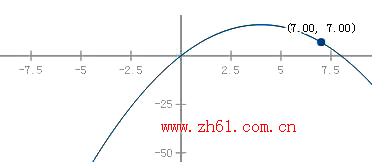
由(t(8-t))'=8-2t=0,求得当t=4m时,物体的最大速度是16m/s。速度v∈[0,16],时间[0,8],路程S粗略估计应该小于16*8=128m。

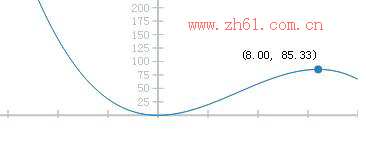
S(t)=F(t)=∫(t(8-t)dt=4t²-1/3t³
上式符号∫表示不定积分,表达式∫(t(8-t)dt表示求函数t(8-t)的反导数或不定积分。
S=4t²-1/3t³=4*8²-1/3*8³=85.33m
reference:
「微积分基本定理」图解普林斯顿微积分读本14
www.zh61.com.cn:微积分的本质,积分,导数的基本定理
www.zh61.com.cn:积分与微积分基本定理,积分是什么?
微积分基本定理(一)
之微积分基本定理(二)
单维彰:微积分入门
-End-

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底