牛顿-莱布尼兹公式(Newton-Leibniz formula),通常也被称为微积分基本定理,揭示了定积分与被积函数的原函数或者不定积分之间的联系。
牛顿-莱布尼茨公式的内容是一个连续函数在区间 [ a,b ] 上的定积分等于它的任意一个原函数在区间[ a,b ]上的增量。牛顿在1666年写的《流数简论》中利用运动学描述了这一公式, [2] 1677年,莱布尼茨在一篇手稿中正式提出了这一公式。
因为二者最早发现了这一公式,于是命名为牛顿-莱布尼茨公式。
牛顿-莱布尼茨公式给定积分提供了一个有效而简便的计算方法,大大简化了定积分的计算过程。
定义
如果函数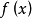 在区间
在区间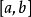 上连续,并且存在原函数
上连续,并且存在原函数 ,
,
则

弱化条件
如果函数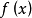 区间
区间  上有定义,并且满足以下条件:
上有定义,并且满足以下条件:
(1)在区间 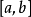 上可积;
上可积;
(2)在区间 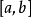 上存在原函数
上存在原函数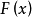 ;
;
则
推导一
定义一个变上限积分函数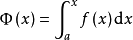 ,让函数
,让函数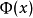 获得增量
获得增量 ![]() ,则对应的函数增量
,则对应的函数增量
证毕。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底