第三章 极限导论

3.1 极限: 基本思想

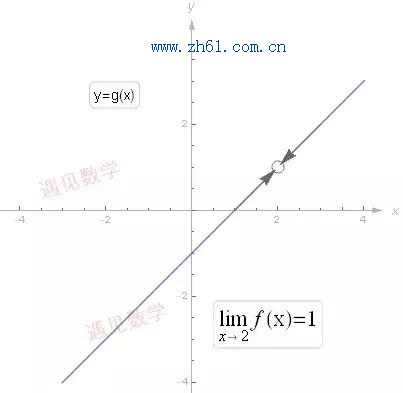
从一个非常奇怪的问题开始: ：以 f(x)=x-1f(x)=x-1 为例, 当 x 非常非常接近于 a, 但不等于 a 时, f (x) 是什么样子的?

极限描述了函数在一个定点附近的行为, 对于上图极限表示式子是说, 当 x 接近于2 时, f(x) 接近于1. 事实上, 我们可以将x 替换成其他任意字母, 上式仍然成立. 也即是变量 x 只是一个哑元(dummy variables, 虚拟变量).

注:哑元(dummy variables, 虚拟变量), 就是只是在过程中会用到, 结果里不可能包含这个虚拟变量, 所以用什么符号来表示都无所谓了.

3.2 左极限和右极限

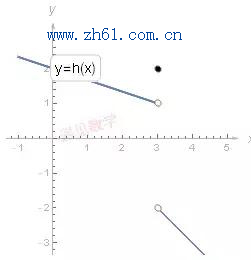
再来看下图 h (x) 在 x = 3 附近的图形.

可以看到h (x) 在x = 3 的左极限(Left-hand limit)等于1, 另一方面, 从右往左的话, 右极限(Right-hand limit)等于 -2.

通常的双侧极限(Two-Sided Limits)在 x = a 处存在, 仅当左极限和右极限在 x = a 处都存在且相等! 用数学语言描述就是

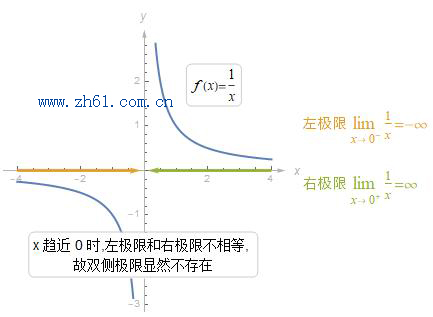
3.3 何时不存在极限

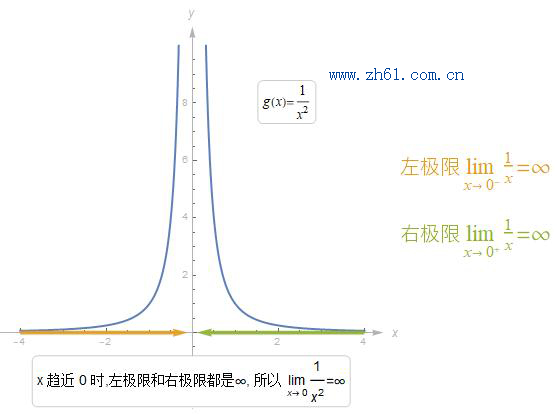
由于左极限和右极限不相等, 故双侧极限显然不存在. 再来考虑考虑函数 g(x)=1x2g(x)=1x2, 图像如下:

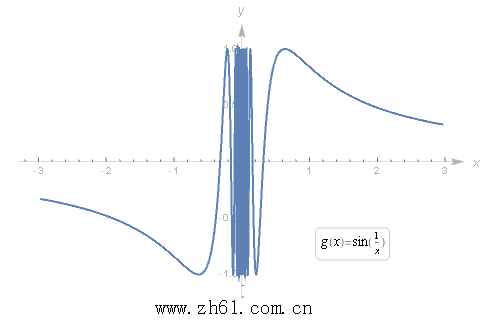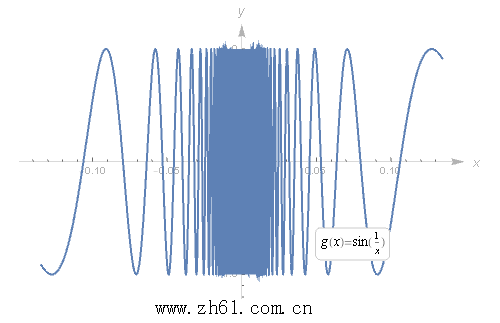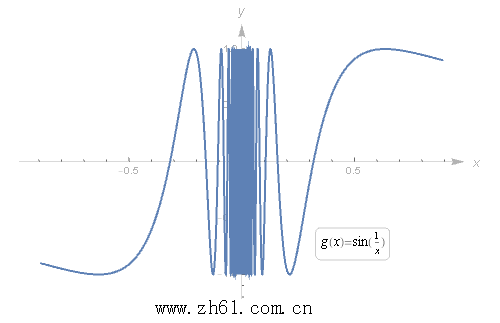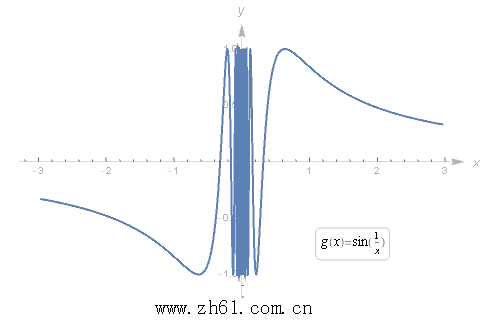
左右极限不存的情况, 比如下面例子函数g(x)=sin(1x)g(x)=sin(1x) . 当接近于 0 的时候, 会在 1 和 -1 直接来回震荡. 所以说极限不存在(DNE).

或者我们观看下面动画来放大图形进行观察:

3.4 在 ∞ 和 -∞ 处的极限

当 x 趋于 ∞ 时候, 函数的变化究竟是如何, 比如当 x 很大的时候, f(x) 变得非常接近于 L, 数学形式为:

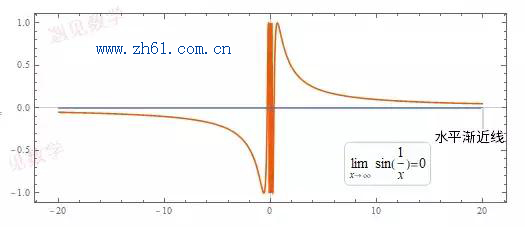
再来回顾下上面的函数 g(x)=sin(1x)g(x)=sin(1x) , 当 x 趋近无限的时候, 函数会非常接近 0 . 所以在 y = 0 处有一条水平渐近线.

3.6 三明治定理(Squeeze theorem)

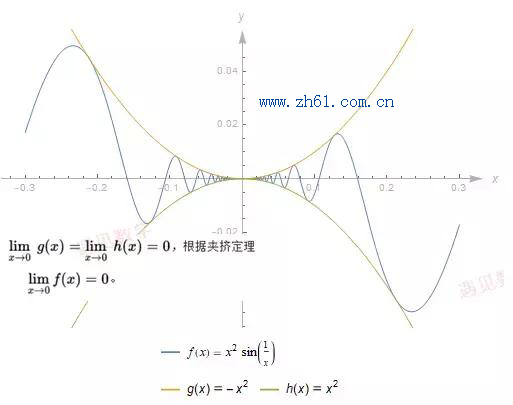
三明治定理(夹逼定理, 或夹挤定理)是有关函数极限的定理。它指出若有两个函数在某点的极限相同，且有第三个函数的值在这两个函数之间，则第三个函数在该点的极限也相同.

3.7 极限的基本类型小结

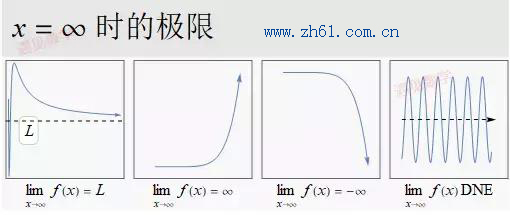
这里只总结列举两种情况的: 在 x = a 时的双侧极限和 x 趋近 ∞ 的情况.

「予人玫瑰, 手留余香」

您能帮助[遇见数学]更快发展吗? 感谢您转发支持!