[遇见数学] 基于风靡美国《普林斯顿微积分读本》一书所制作图解系列, 内容章节安排完全按照此书推进, 提供更多的图像和动画来让读者体会微积分的无穷魅力, 建议配合原书来学习. 还请各位老师和读者多多指导, 方便我们进一步改进.
1.1 函数
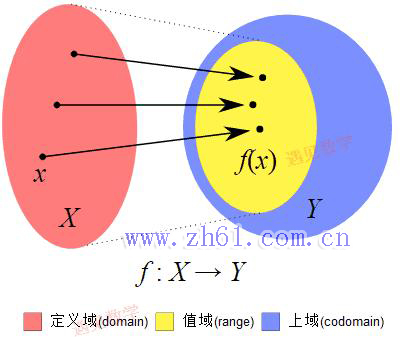
定义函数是将一个对象转化为另一个对象的规则. 起始对象称为输入, 来自称为定义域的集合. 返回对象称为输出, 来自称为上域的集合.
一个函数必须给每一个有效的输入指定唯一的输出.
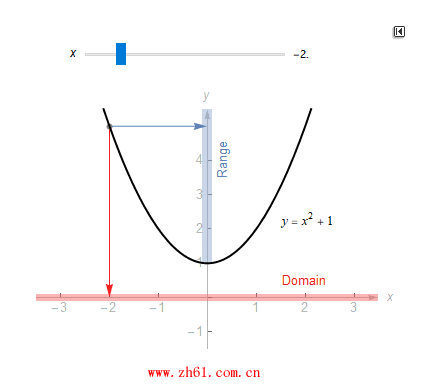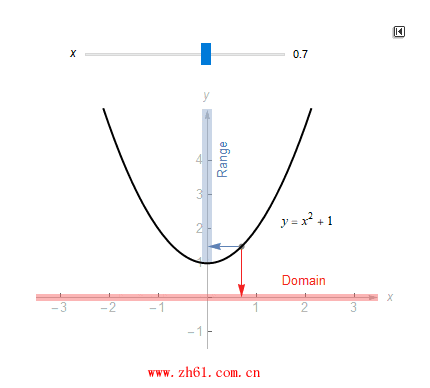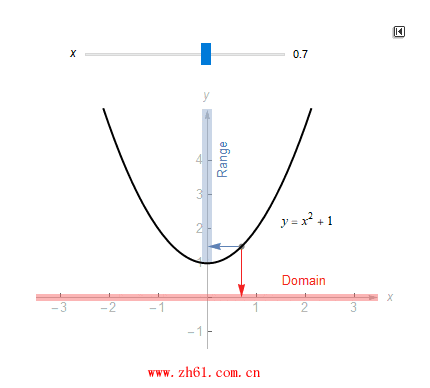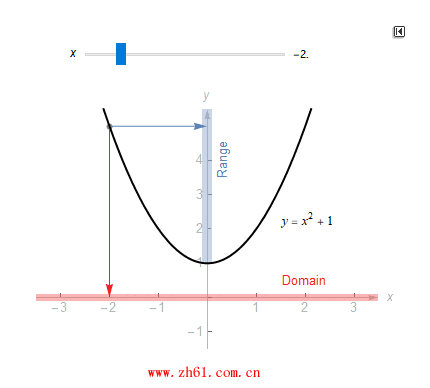
值域实际上是上域的一个子集. 上域是可能输出的集合, 而值域则是实际输出的集合. 如 f(x)=x2f(x)=x2 , 其定义域和上域均为 R, 那么其值域是大于等于 1 数的集合, 观察下面的动图:
1.1.1 区间表示法
1.1.4 垂线检验(Vertical Line Test)
如果你有某个图像并想知道它是否是函数的图像, 你就看看是否任何的垂线和图像相交多于一次. 如果多余一次, 则不是函数的图像.
1.2 反函数
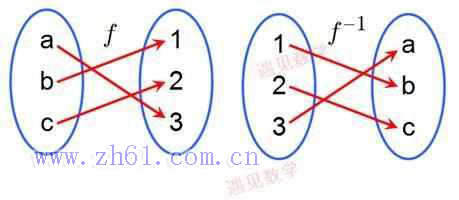
定义反函数为对一给定函数做逆运算的函数. 也就是从输出y 出发, 这个新的函数发现一个且仅有一个输入 x 满足 f (x) = y. 这个新的函数称为 f 的反函数, 并写作 f−1f−1.
1.2.1 水平线检验
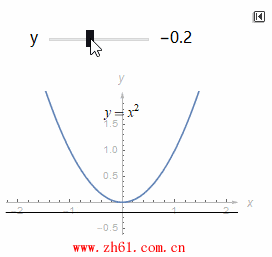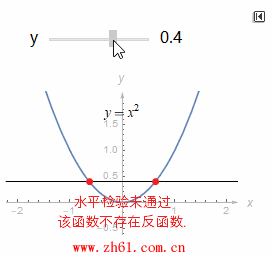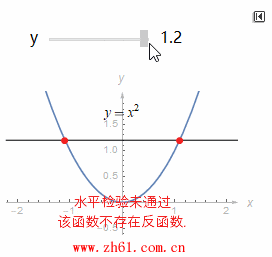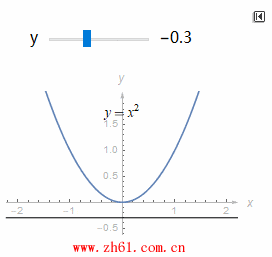
如果每一条水平线和一个函数的图像相交至多一次, 那么这个函数就有一个反函数.
1.2.3 限制定义域
如果水平线检验失败因而没有反函数, 可以限制函数的定义域, 使之满足水平线检验. 比如将 g(x)=x2g(x)=x2 的定义域缩减为 [0,∞) , 就满足水平线检验, 也有了反函数.
1.3 函数的复合
复合函数指一个将第一个函数作用于参数, 然后再将第二个函数作用于所得结果的函数. f 是 g 与 h 的复合函数写成 f = g ∘ h .
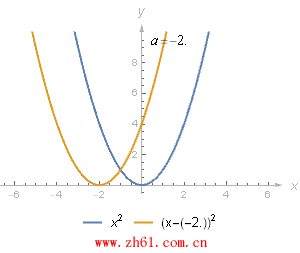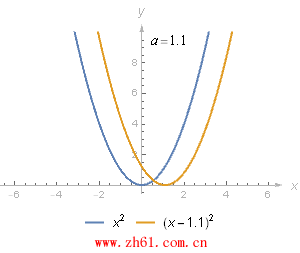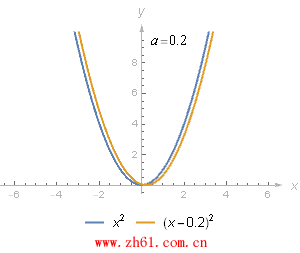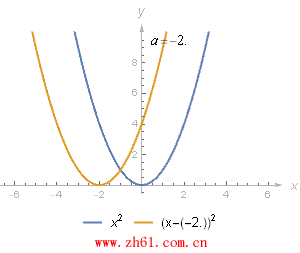
复合函数另一个简单但重要的例子是, 将函数 f 和 g(x) = x-a(a 是常数) 进行复合. 对复合得到的新函数 h(x) = f(x-a), 需要关注的是新函数 y = h(x) 和函数 y = f(x) 的图像是一样的, 只不过 y = h(x) 的函数图像向右平移了a 个单位.
类似地, y=(x+2)2y=(x+2)2 的图像是将 y=x2y=x2 的图像向左平移 2 个单位, 可把 (x+2) 理解为 (x -(-2))
1.4 奇函数和偶函数
一些函数具有对称性, 偶函数的图像关于y 轴具有镜面对称性, 即对所有的 x , f 都有 f(-x) = f(x) . 而奇函数是关于原点对称, 即奇函数的图像关于原点有180°的点称性.
1.5 线性函数的图像
形如f(x) = mx + b 的函数叫作线性函数. 图像为一条直线, 斜率为 m.
斜率m 为正数, 那么你正在上山. m 越大, 这段上坡就越陡. 相反, 如果m 为负数, 那么你正在下山. m 的数值越小(即绝对值越大), 这段下坡也就越陡. 如果斜率为0, 这直线就是水平的.
直线方程的点斜式:如果已知直线通过点 (x0,y0)(x0,y0), 斜率为 m, 则它的方程为 y-y0=m(x-x0)y-y0=m(x-x0)
1.6 常见函数及其图像
(1) 多项式
anxn+an−1xn−1+...+a1x+a0anxn+an−1xn−1+...+a1x+a0 一般的多项式的图像是很难画的. 不过, 多项式的图像左右两端的走势倒是容易判断. 这是由最高次数的项的系数决定的 anan, 该系数叫作首项系数.
(2) 有理函数
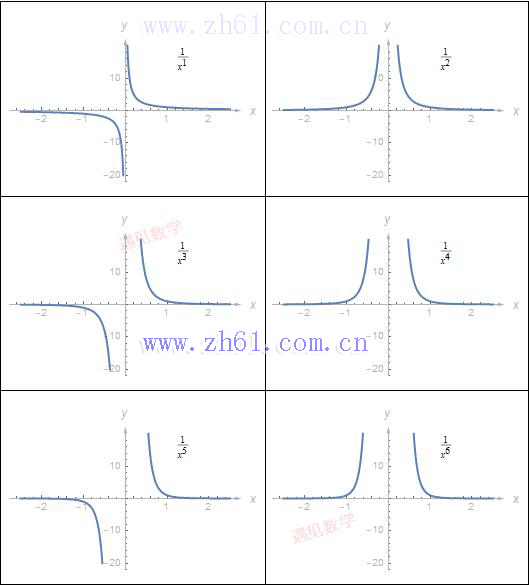
形如 p(x)/q(x) 其中 p 和 q 为多项式的函数, 叫作有理函数. 一个简单的例子是 1/(x^n), 其中n 为正整数, 观察下面奇次幂和偶次幂的图像:
(3) 指数函数和对数函数
请查看【自然常数E的故事】和【延长了天文学家寿命的对数函数】文章
第一章《函数、图像和直线》完
参考资料: 《普林斯顿微积分读本》、维基百科
「予人玫瑰, 手留余香」
非常感谢您关注并支持本号更快发展!

 更多
更多


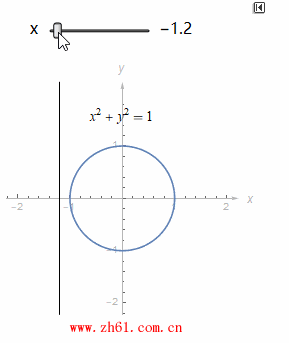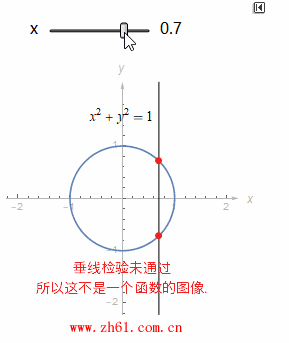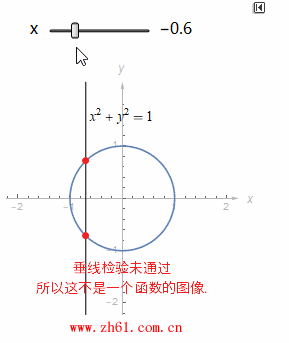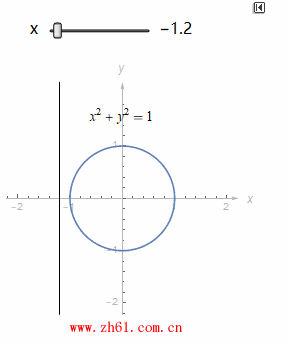



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底