请关注 [遇见数学] 今日头条收看更多关于数学文章的资料和视频!
[遇见数学] 基于风靡美国《普林斯顿微积分读本》一书所制作图解系列, 内容章节安排完全按照此书推进, 提供更多的图像和动画来让读者体会微积分的无穷魅力, 建议配合原书来学习. 关注 [遇见数学] 收看更多图解数学课程!
第 17 章 微积分基本定理(The Fundamental Theorems of Calculus)
这一章我们将要学习:
-
用另一个函数的积分形式来表示的函数;
-
第一基本定理, 以及反导数的基本思想;
-
第二基本定理;
-
不定积分和它们的性质.
17.1 用其他函数的积分来表示的函数
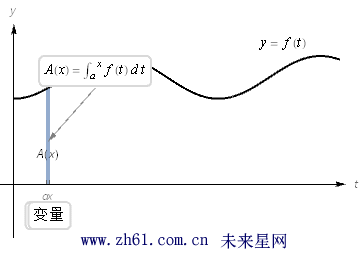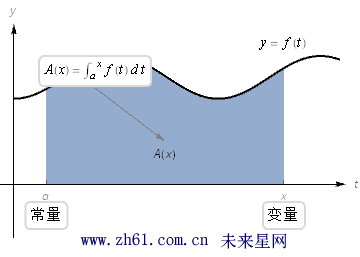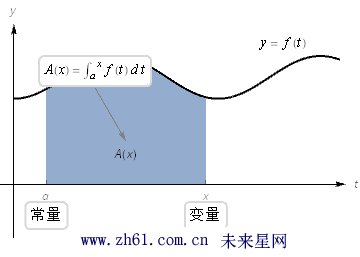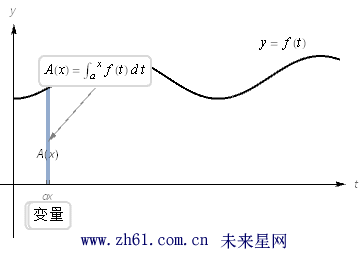
考虑积分下面积分式子实际上是一个以积分上线 x 为变量的函数, 这就有
观看下面的动画:
17.2 微积分的第一基本定理(The First Fundamental Theorem)
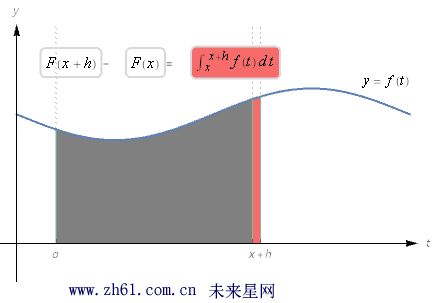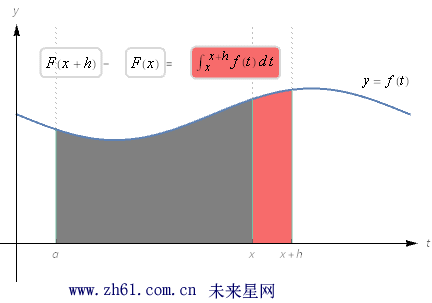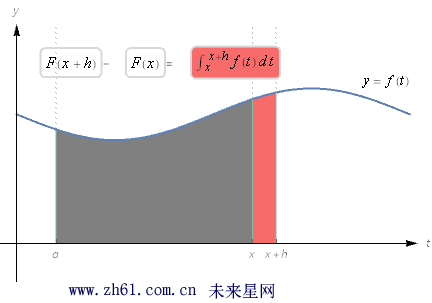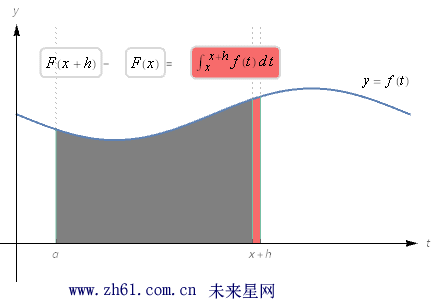
观察下面的图形:
上图淡红色的阴影部分, 当 h 很小的时候几乎为小竖条, 所以可以用计算长方形面积的方法来估算该竖条的面积, 它的底从x 到x+h, 高从0 到f(x), 所以面积是 h*f(x) , 也就是:
微积分的第一基本定理:如果函数f 在闭区间 [a,b] 上是连续的, 定义F 为
则 F 在开区间 (a,b) 内是可导函数, 而且 F'(x)=f(x)
反导数的引入(Introduction to antiderivatives)
假设 f(t)=t2, a=0f(t)=t2, a=0 所以有
微积分的第一基本定理告诉我们 F'(x) = f(x). 因为f(t) = t2t2, 所以有f(x) =x^2; 也就是说, F'(x) = x^2. 换一种说法, 函数 F 的导数为 x^2. 我们说 F 是 x^2 的反导数(关于x).
17.3 微积分的第二基本定理
微积分的第二基本定理:如果函数 f 在闭区间[a, b] 上是连续的, F 是 f 的任意一个反导数(关于x), 那么有
17.4 不定积分(Indefinite Integrals)
到目前为止, 我们使用两种不同的方法计算定积分:黎曼和的极限和反导数.
如果你知道一个函数的导数, 那么就会很快求出这个导数的反导数. 具体情况是:
不定积分没有积分上下限, 而定积分有.
定积分是一个数, 它表示由曲线 y=f(x), x 轴以垂线 x=a 和 x=b 所围成的面积;不定积分是一个函数的集合. 这个集合由函数 f 的所有反导数(关于 x)组成. 例如:
不定积分的两个性质:
17.6 怎样解决问题:微积分的第二基本定理
(End)
和自己最好的朋友们一起来遇见数学!

 更多
更多
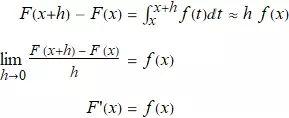
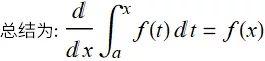
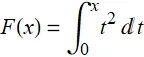


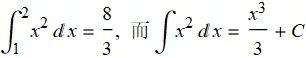
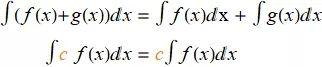

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底