科里奥利力不是真实存在的力(不像万有引力、电磁力、压力、摩擦力等等),这种力之所以会产生,是因为参考系的旋转。其本质来源于物体的惯性(角动量守恒)。
而旋转的参考系并不是惯性系(即使物体不受力,运动状态也会发生变化),所以如果想像惯性系中那样处理问题,就需要假想某种力作用在物体上。
下面来简单推导科里奥利力的形式:
为了好理解,想象一个小球在你正前方,以一定速度向前运动,你在原地旋转,你会看到,小球不光在围绕你转圈,而且离你越来越远,角动量越来越大,但并没有力矩施加在小球上。在旋转参考系中,我们需要假想出一种力——科里奥利力,在科氏力的作用下,角动量不断增大。
上面举的小球的例子中,小球没有跟随参考系一起旋转,但我们常见的都是跟随参考系一起旋转的物体,比如河流偏转,台风旋向等,都跟随地球一起旋转。
就拿北半球的河流举例,假设河流是从北向南流,在流动的过程中,河流距离旋转轴的距离越来越远,如果河流流向不改变,那么角动量是增大的,为了保证角动量不变,河流会往西偏以减小随地球旋转的速度。
这种偏转之所以难以理解,是因为我们习惯性地假设大地参考系是惯性系,其实不然,我们是随地球一起转动的,所以看到河流偏转感到奇怪(因为并没有受到力的作用)。在地球之外的惯性系中很容易理解这一点,其实就是河流中的水围绕地球转动,由于惯性需要保证角动量守恒。
但我们身在旋转参考系之中,如果想要当作惯性系处理,就需要假想出科里奥利力来描述这一看似奇怪的现象。
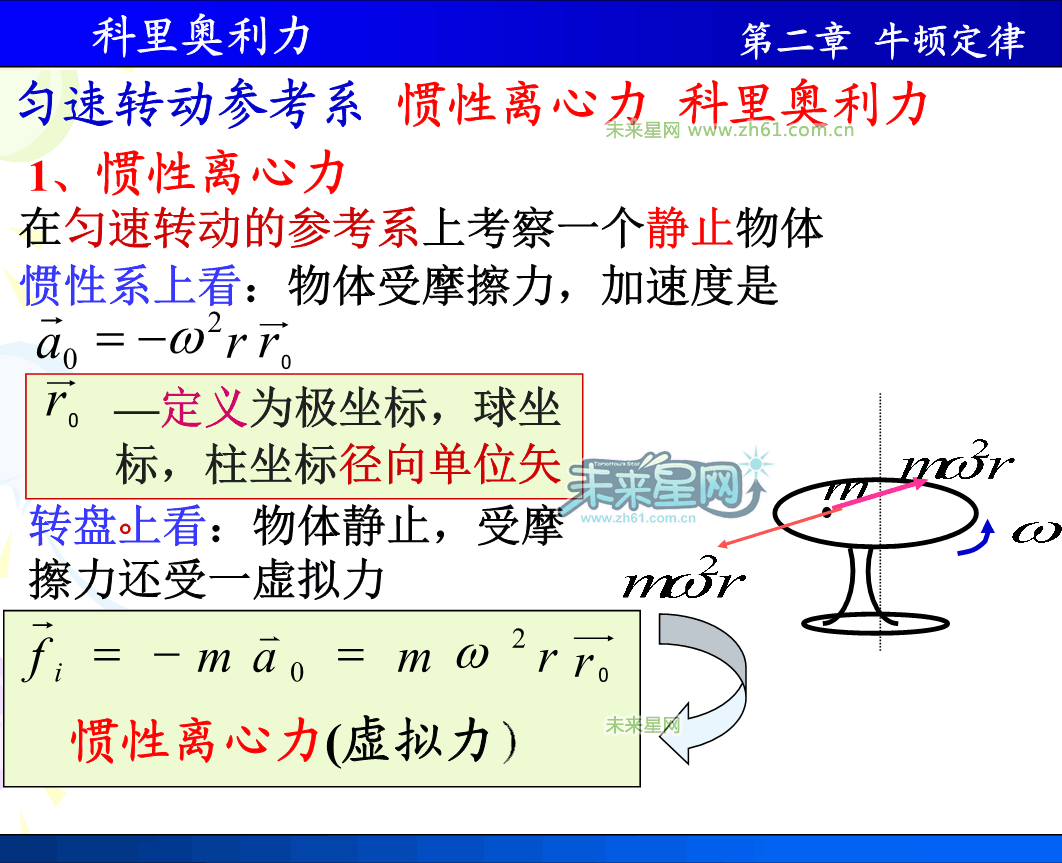
当你坐在旋转木马上的时候,会感受到仿佛有一股力,总要把你从座位上扯下来。但我们知道,跟直观感受相反,其实如果没有力的话,我们本来应该直线运动;而正是座位顶住我们的力,使得我们跟着木马一起做圆周运动。而跟这个力大小相等方向相反的那个所谓“离心力”,其实是并不存在的,仅仅由于改变了参考系才出现,所以称这种力为“惯性力”——由惯性参考系变换到非惯性参考系出现的力。
那么你设想在太空中转动的地球上,你在北半球从北向南走一小段路,如果是在太空这个惯性系中,走直线的话(地球上足够小的一段路可以近似看做是直线),应该是从A到B。但因为你跟着地球一起转动,所以B的位置发生了变化,变成了C。于是惯性的速度Vab变成了在地球这个非惯性系中的Vac,两个速度之间的向量差Vbc,求导后就可以表示为一个跟上面离心力类似的惯性力,也就是科里奥利力。
总结一下,所谓科里奥利力,其实就是由于地球拉着你转,使你运动轨迹跟惯性系下理想的轨迹产生偏移,而“错觉”出来的力。

 更多
更多
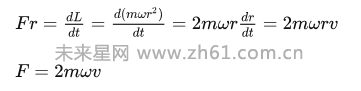
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底