神奇的流体
科里奥利(Coriolis,Gustave Gaspard de,1792~1843)是法国物理学家。1836年当选为法国科学院院士,1838年起在巴黎综合工科学校教授数学物理。1835年,科里奥利在《物体系统相对运动方程》的论文中指出:如果物体在匀速转动的参考系中作相对运动,就有一种不同于通常离心力的惯性力作用于物体,并称这种力为复合离心力。后人以他的名字将该复合离心力命名为“科里奥利力”。
※※科里奥利力※※
科里奥利力简称“科氏力”,主要是由坐标系的转动与物体在动坐标系中的相对运动引起的,表达式为Fc=2mV×ω。
其中,Fc为科氏力,m为运动物体质量,V为运动物体的矢量速度,ω为旋转体系的矢量角速度,×表示两个向量的叉乘。
从式中可看出,当物体运动方向与旋转轴方向平行时科氏力为零。
注:科氏力与离心力一样,都不是真实存在的力,而是惯性效应在非惯性系内 (本文默认为旋转系统) 的体现。也就是说,从惯性系的角度看,科氏力是不存在的。
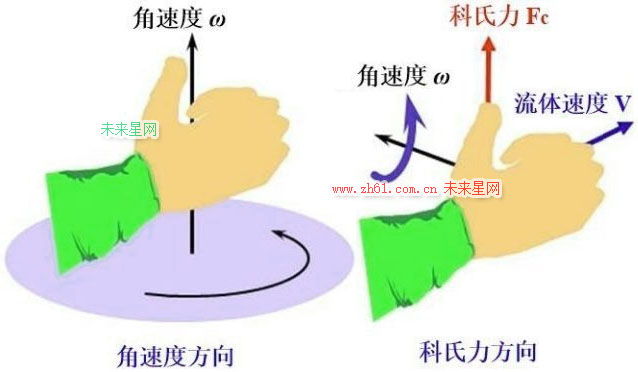
※※科氏力方向※※
在判断科氏力Fc方向前,需先判断角速度ω的矢量方向,两者都遵循右手螺旋法则。因此,分为两个步骤:
1、角速度方向:右手(除大拇指外)手指顺着转动的方向朝内弯曲,大拇指所指的方向即角速度的矢量方向。
2、科氏力方向:右手(除大拇指外)手指指向(非惯性系中)物体运动方向,再将四指绕向角速度方向,拇指所指方向即科里奥利力方向。
在北半球,沿着水冲向漏水口的方向,水流受到向右的科氏力,因而俯视角度看就是逆时针漩涡,同样在南半球则是顺时针漩涡。

 更多
更多

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底