万有引力定律的推导过程

①太阳和地球之间的引力提供地球绕太阳做匀速率圆周运动的向心力；

②向心力用带有周期的公式来描述；

③得出：引力与地球的质量成正比，与距离的平方成反比；

④再利用牛顿第三定律得出：引力还与太阳的质量成正比；

⑤最后用地球和月亮之间的引力也满足此关系的佐证，得出万有引力定律。

万有引力定律推导公式是什么

根据开普勒的三定律以及牛顿第三定律得出.

具体如下;F引= F向=mw2r＝mv2/r再由线速度与周期的关系得到

F引=m(2πr/T)2/r= 4π2mr/T2

F引=4π2mr/T2= 4π2(r3/T2) m/r2

F引=4π2km/r2

所以可以得出结论：太阳对行星的引力跟行星的质量成正比,跟行星到太阳的距离的二次方成反比.

即：F∝m/r2

牛顿根据牛顿第三定律大胆的猜想：既然太阳对行星的引力与行星的质量成正比,也应该与太阳的质量成正比.

F引 ∝ Mm/r2

写成等式：F引= GMm/r2

万有引力定律适用条件是什么

中学物理中的万有引力定律只适用于两个质点间的万有引力计算,若不能将物体看作质点,则定律不成立,或者说需要用微分法将物体分解成很多个质点,再依次求各质点间万有引力,然后将这些引力求矢量和,实际上就是中学阶段不能计算.

广义上讲,万有引力定律是适用于一切物体间的引力计算的.

万有引力的适用范围

万有引力定律：自然界中任何两个物体都是相互吸引的，引力的大小跟这两个物体的质量乘积成正比，跟它们的距离的二次方成反比。

由此得：

1，万有引力不是说所有的物质都只有引力，比如：两团气体不一定会相互吸引，高能粒子不一定会互相吸引。

2，万有引力只是说物体之间存在着引力。当然，并非是所有物体之间都存在引力，比如：同性磁铁就是相斥的。

这上述两条就是规定了万有引力适用的范围。

万有引力公式适用于哪些情况

①严格来说只适用于质点间的相互作用；

②两个质量分部均匀的球体间的相互作用,也可用本定律计算,（其中r是两个球心距离）；

③一个均匀球体与球外一个质点的万有引力也适用（r是球心到质点的距离）；

④当两个物体间的距离远远大于物体自身大小时,公式也近似适用,（其中r是两物体质心间距离）；

万有引力是由于物体具有质量而在物体之间产生的一种相互作用。

它的大小和物体的质量以及两个物体之间的距离有关。物体的质量越大，它们之间的万有引力就越大；物体之间的距离越远，它们之间的万有引力就越小。

· 万有引力是谁发现的

定义

万有引力定律：自然界中任何两个物体都是相互吸引的，引力的大小跟这两个物体的质量乘积成正比，跟它们的距离的二次方成反比。

发现过程

年轻的伊萨克·牛顿坐在自己家的花园中，一个苹果落下来砸到他的头上，他忽然灵感乍现，想出了万有引力定律。

牛顿又进一步发展他的想法。他比较了掉落中的苹果与掉落中的月亮，后来牛顿了解到，如果月亮没有朝著地球掉落的话，它将会做直线运动，最后则会脱离绕地轨道，所以他认为月亮正绕著地球而掉落(月球可是很认真的掉唷)。因此，月亮必定掉落在那条没受到外力时应该会走的下方。

牛顿大胆地假设，月球在重力的吸引下，只是一个绕著地球转的抛体而已。至於月球的切线速度是怎麽来的，可能就是在宇宙大霹雳、创世之时就决定了，而月球的切线速度大小将会决定它绕地球的轨道是圆形、椭圆形、抛物线、双曲线或是撞上地球。

科学意义

万有引力定律的发现，是17世纪自然科学最伟大的成果之一。它把地面上物体运动的规律和天体运动的规律统一了起来，对以后物理学和天文学的发展具有深远的影响。它第一次解释了（自然界中四种相互作用之一）一种基本相互作用的规律，在人类认识自然的历史上树立了一座里程碑。

·     知识拓展：

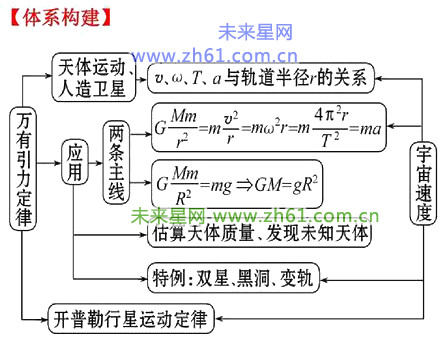
万有引力定律在高中物理中的地位：

在万有引力定律之前，学生应对力、质量、速度、加速度、向心力和向心加速度等物理概念有较好的理解，并掌握自由落体、抛体和匀速圆周运动的规律，能熟练运用牛顿运动定律解决动力学的基本问题。将万有引力定律与圆周运动知识相结合，可以讨论许多涉及天体和人造卫星运动等方面的实际问题。如太阳、地球及其它行星的质量、密度；计算人造卫星的轨道、周期等一系列参数，包括地球的同步卫星等；反过来还可推证开普勒行星运动定律。