角动量守恒定律，在宇宙天体的形成过程中非常重要，比如说我们的太阳系，在太阳系诞生初期，太阳把角动量分给八大行星，让它们一直旋转至今。而角动量守恒在我们日常生活中也很常见。
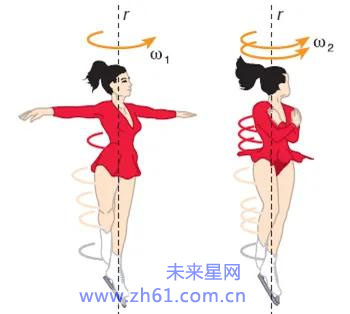
比如说花样滑冰运动，运动员在旋转过程中通常会先伸开双臂，然后收回双臂，从而让自己的转速加快，这就是角动量守恒的直接体现！

什么是转动惯量？

　　转动惯量是大学物理中一个十分重要的知识点。下面是由未来星网编辑为大家整理的“转动惯量的定义以及计算公式”，仅供参考，欢迎大家阅读本文。

　　转动惯量

　　转动惯量(Moment of Inertia)，又称质量惯性矩，简称惯距，是经典力学中物体绕轴转动时惯性的量度，常用用字母I或J表示。转动惯量的SI单位为kg·m²。对于一个质点，I=mr²，其中，m是其质量，r是质点和转轴的垂直距离。

　　和线性动力学中的质量相类似，在旋转动力学中，转动惯量的角色相当于物体旋转运动的惯性，可用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

　　对于规则物体，其转动惯量可以按照相应公式直接计算;对于外形复杂和质量分布不均的物体，转动惯量可通过实验方法来测定。实验室中最常见的转动惯量测试方法为三线摆法。

　　转动惯量计算公式

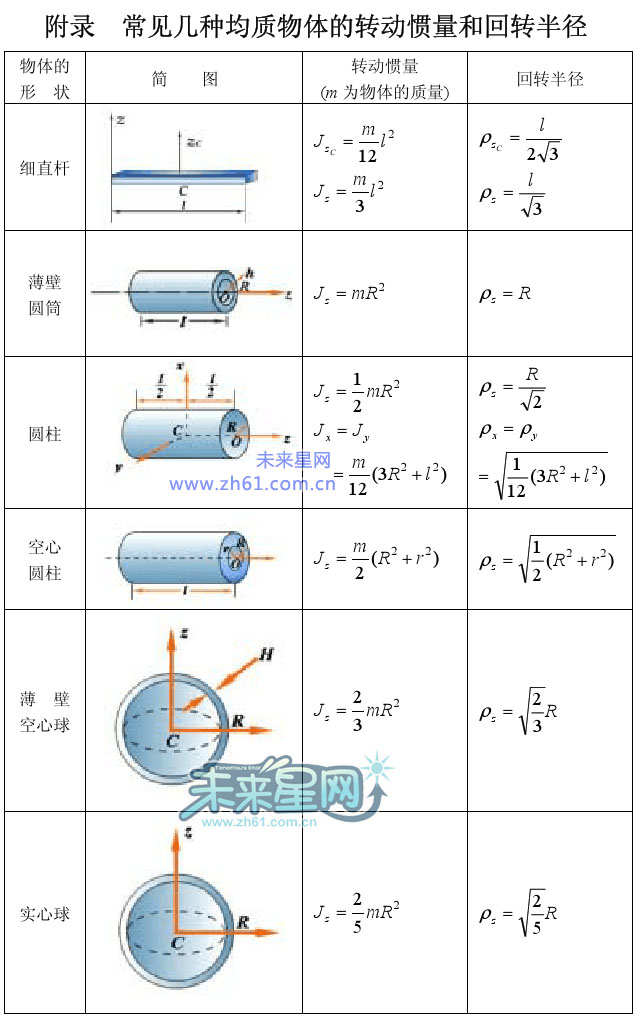
　　1、对于细杆：

　　当回转轴过杆的中点(质心)并垂直于杆时I=mL²/I²;其中m是杆的质量，L是杆的长度。当回转轴过杆的端点并垂直于杆时I=mL²/3;其中m是杆的质量，L是杆的长度。

　　2、对于圆柱体：

　　当回转轴是圆柱体轴线时I=mr²/2;其中m是圆柱体的质量，r是圆柱体的半径。

　　3、对于细圆环：

　　当回转轴通过环心且与环面垂直时，I=mR²;当回转轴通过环边缘且与环面垂直时，I=2mR²;I=mR²/2沿环的某一直径;R为其半径。

　　4、对于立方体：

　　当回转轴为其中心轴时，I=mL²/6;当回转轴为其棱边时I=2mL²/3;当回转轴为其体对角线时，I=3mL²/16;L为立方体边长。

　　5、对于实心球体：

　　当回转轴为球体的中心轴时，I=2mR²/5;当回转轴为球体的切线时，I=7mR²/5;R为球体半径。