伯努利原理
伯努利原理简单来说就是,在流体中,速度大,压强就小,速度小,压强就高,当然也有它的适用条件,就是所谓的理想流体,第一就是流体不随时间变化,第二就是无摩擦,第三就是不可压缩,第四就是流体沿着流线运动,流线彼此不相交。
(伯努利方程)用数学公式表达就是
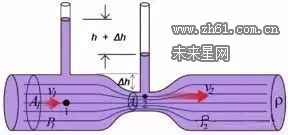
P是压强,ρ是密度,v是速度,h是高度,C就是常数。
伯努利方程的应用:
文丘里流量计
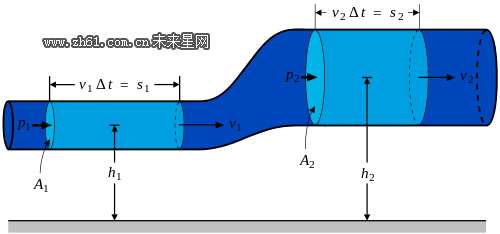
文丘里流量计是测量流体压差的一种装置。它是一个先收缩而后逐渐扩大的管道。在收缩段的直管段截面1和截面2两处,测量静压差和两个截面的面积,并用伯努利方程即可计算出通过管道的流量。 需要注意的是,由于收缩段的能量损失要比扩张段小得多,所以不能用扩张段的压强来计算流量,以免增大误差。
拉瓦尔喷管(亦称渐缩渐阔喷管)是瑞典人拉瓦尔在1883年在蒸汽涡轮机上应用的喷管。喷管的截面积首先变小然后再变大,从中间通过的气体可被加速到超音速,而并不会产生撞击。气体在截面积最小处恰好达到声速。
拉瓦尔喷管的原理。第一节,截面小处流速大,截面大处流速小的原理,因此气流不断加速。当到达窄喉时,流速已经超过了音速。而跨音速的流体在运动时却不再遵循截面小处流速大,截面大处流速小的原理,而是恰恰相反,截面越大,流速越快。
也就是说前半段为伯努利方程可以解释,后半段,需要跨声速流来解释。
个人理解,因为空气的可压缩性,会形成一个阻力,也就是音障。
打个比方来说,如果我的速度达到了音速,空气与我的相对速度太快,被“压”实了。在音速状态下,我们可以“摸到空气”,就像液至固体的状态,而且因为音速可以靠更强大的推力超越,所以我们可以像跳水时,穿过“水面”一样,穿过“空气面”。
人们在实践中发现,在飞行速度达到音速的十分之九,即马赫数M0.9空中时速约950公里时,局部气流的速度可能就达到音速,产生局部激波,从而使气动阻力剧增。
而穿过“空气面”的气体,就达到了跨声速流体的状态。如果这时,这个“跨声速流体”的气体要减速,会被后续的气体“推着”,也就是要降到声速以下,会被后续的声障推着,只有扩口足够大,向四方扩散的阻力足够小,才能顺利将速度降下来。否则,拉瓦尔管只要扩口不够大,气体可以无限扩张,气体流速不会降到声速以下。所以截面越大,流量越大。(不过我认为,压力应该是变小了的。)

 更多
更多


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底