在几何学中，规则图形的面积和体积非常容易计算，我们在初高中都已经掌握了这些基本的计算公式，如下图像所示

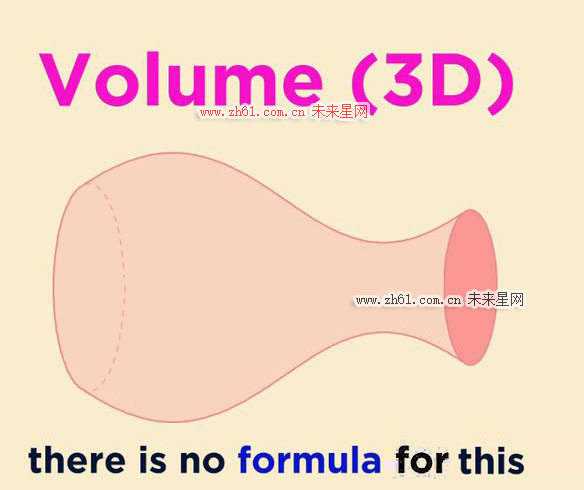
当涉及到曲面时，一般公式的计算方法就会统统失效，这时就需要微积分的知识来完成，如下是一个不规则的曲面，要计算它的体积，一般公式是无法计算的

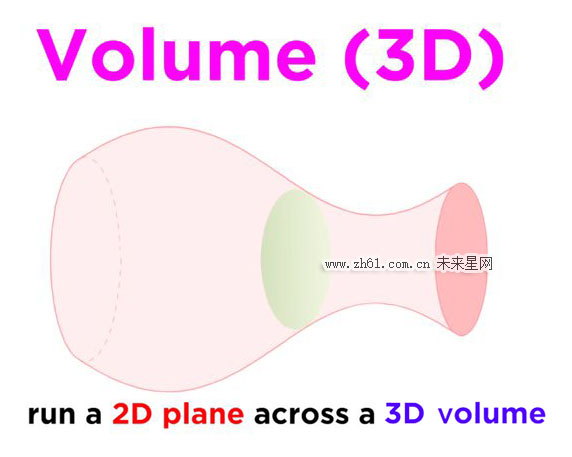
这里我们不是将其分割成无限多的矩形，而是将其分割成无限多的薄片，每个薄片都是一个二维区域，这给我们的计算提供了可能

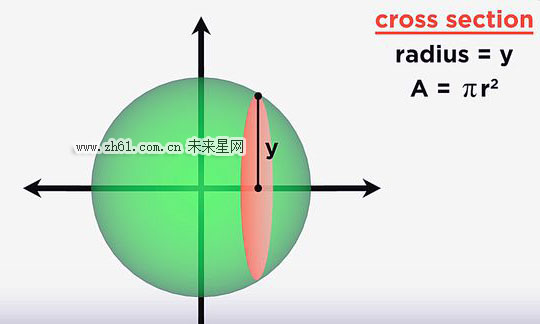
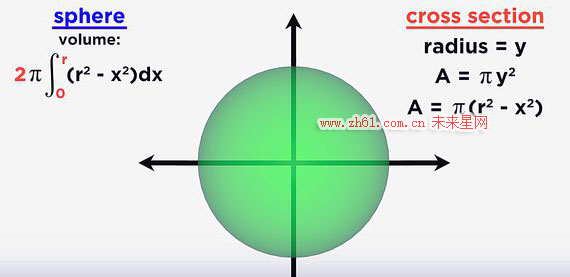
从最简单的球体出发，在水平方向上，我们可以将这个圆切成无限多的薄片，每个圆薄片的半径都对应一个y值

即A=πy^2

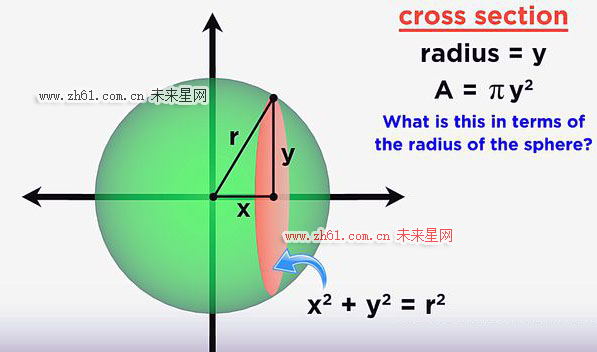
因为圆的面积是πr^2，但球体的的半径是不变的，所以我们可以根据勾股定理作一个直角三角形，得到y=r^2-x^2 如下图所示

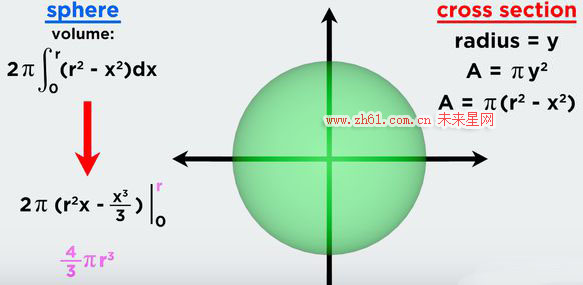
这样就与x建立了联系，且区间是(-r,+r)，因为球体关于y轴对称，所以根据微积分原理我们就得到如下结论

这样最终就得到了球的体积

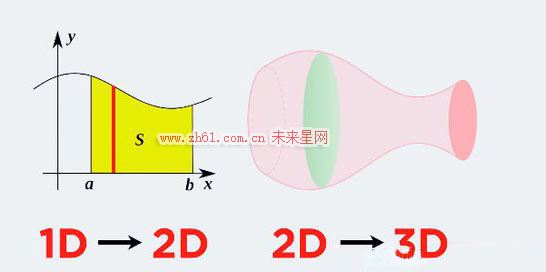
所以无限的二维平面的叠加，就是三维物体的体积，但需要微积分作为桥梁

我们继续延伸，如下是一个X^1/2图形绕x轴旋转产生的不规则物体，如何来计算它的体积呢？

同样采用叠加所有横截面来进行计算

但这里的半径r是X^1/2，所以有关横截面积就是πX

这样我们就得到了（0,1）区间上该物体的体积，如下图所示

这些伟大的发现都是基于牛顿和莱布尼兹的发现