前面我们用微积分计算了不规则图形的体积,它针对的是一个不规则的实体,它是单一的绕X轴或绕Y轴旋转而得到的,比较简单,如果对于的空心的不规则的图形如何来计算它的体积,是本篇要讨论的问题,
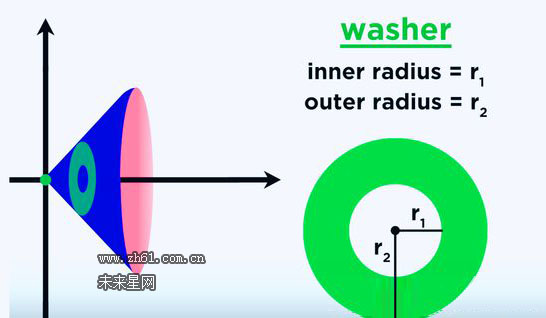
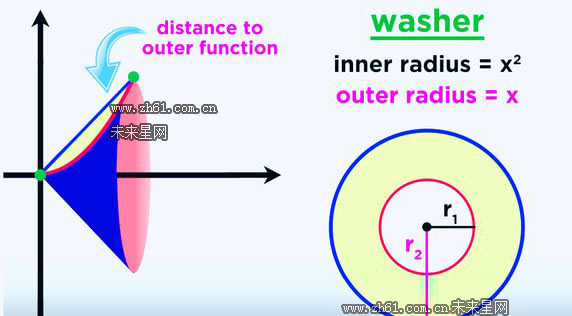
例如如下图:将 其绕X轴旋转,就形成一个空心的垫圈
这个垫圈的横截面就是一个圆环,它有内外径之分,旋转轴到实心开始的地方,我们称它为内径,旋转轴到实心结束的地方,我们称它为外径
图形的内外半径随着X值的变化而变化
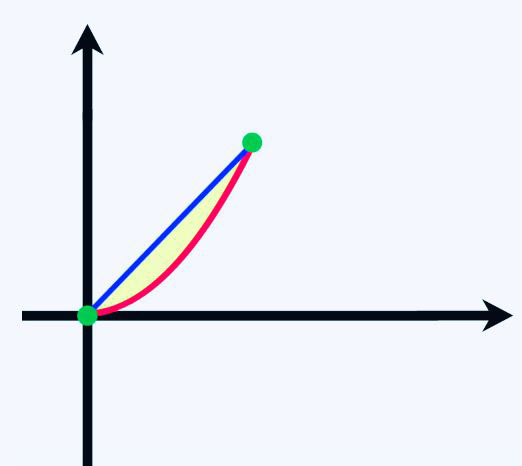
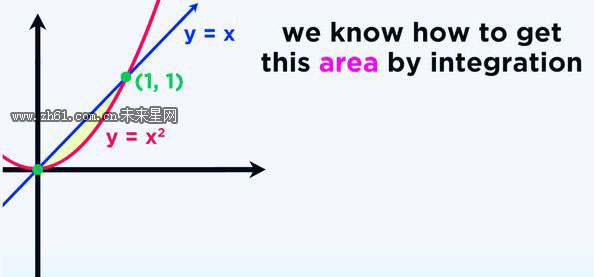
让我们分析Y=X^2,y=x,这两个函数相交的区域形成一个封闭的区间,我们现在通过积分来计算这个区域的面积
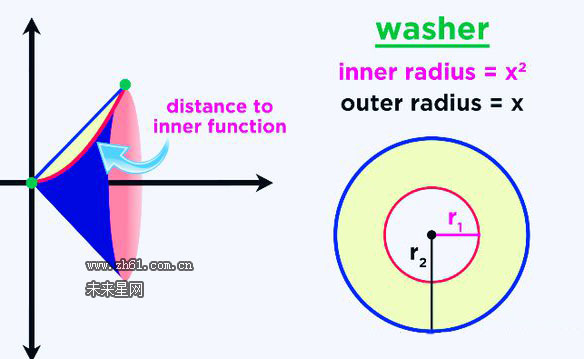
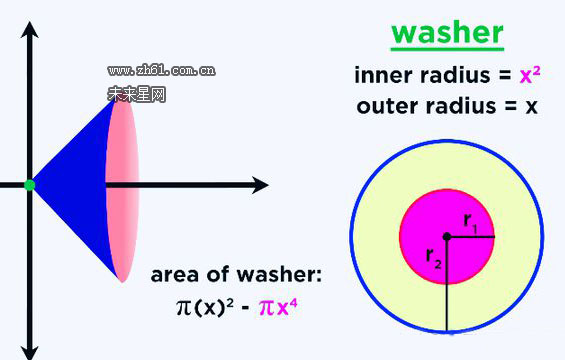
上图绕X轴旋转,立体图中的内半径等于X^2,外半径等于X
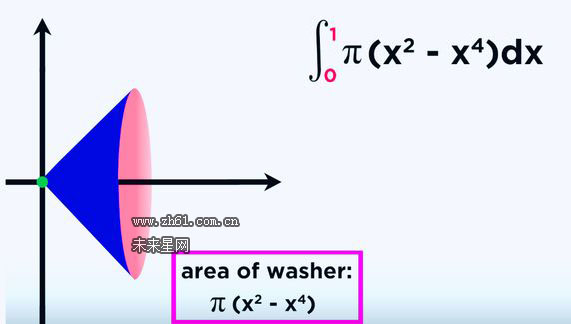
实体横截面区域的面积等于πX^2-π(X^2)^2,也就是大圆的面积减去小圆的面积
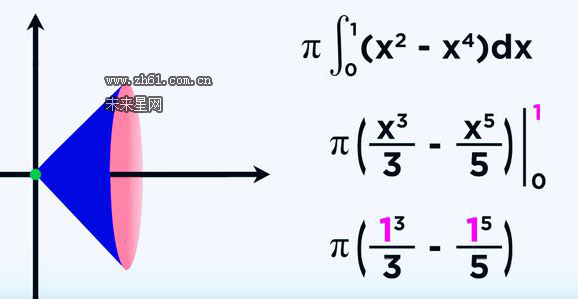
整合重叠区域的面积,0到1区间的黎曼和,即定积分就是我们所求的体积
所以简单的积分计算就得到两个函数之间的区域围绕一个轴旋转时形成的体积
我们可以将相同的区域,绕不同的轴旋转,并获得不同的形状,例如绕Y轴旋转,就会得到这个,并且半径是完全不同的
这时我们就要用不同的函数关系来表示内外半径,但这里的半径是与Y有关,而不是X,但这需要你灵活的思维方式。

 更多
更多



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底