1686 好多人觉得数学没有用,或者用处不大,上学学习的三角函数和二元二次方程组在实际生活中根本应用不到,一般来说,只是在购物的时候用到一些加减法而已。这种想法跟微积分是牛顿和莱布尼茨发明的一样大错而特错。数学是物理的基础,而物理发展则推动了我们的科技,这毋庸置疑,古往今来,绝大多数的发明家首先是一个物理学家。我们的文明发展到今天的地步,亦离开不数学,航海、天文、矿山建设等许多课题都有赖于数学的发展才能得以深入研究。有一个很典型的故事,一个物理系的学生问他的老师:“为什么近一百年来物理学都没有什么惊天动人的建树?”老师想都没想直接回答道:“因为数学没有发展。”这虽然只是一个则故事,真伪难辨,但已经能说明数学的重要性。而数学当中在现实生活中应用最广泛的就是微积分。
微积分的出现解决了一直困惑人们的两个问题:第一是如何计算曲线上任意点的切线,即微分;第二是如何计算任意一块区域的面积,即积分。所以微积分是微分学和积分学的统称。

微积分原理示意图
提到微积分,很多人就头疼。但是学数学绕不开微积分,正如我国一句老话所说,“工欲善其事必先利其器”,微积分就是数学家手里的“利器”,很多研究都是以微积分为基础,其重要性不言而喻。提到微积分,很多人以为就是函数,其实微积分是一个统筹的概念,主要包括极限、微分学、积分学及其应用,其中微分学包括求导数的运算,是一套关于变化率的理论,积分学包括求积分的运算。提到微积分,很多人第一时间就想到牛顿和莱布尼茨,认为是这两个人发明创建了微积分,其实不然,实际上微积分是经过几代数学家的持续努力和研究,经过漫长时间的发展演变才得以形成。

牛顿画像
牛顿和莱布尼茨的贡献在于将微积分更加系统和成熟地表述出来,形成一种理论学科。这些人包括费马、笛卡尔、罗伯瓦、笛沙格、巴罗、瓦里士、开普勒、卡瓦列利等知名数学家,他们所提出的理论为微积分的创立做出了贡献。费马曾经提出用水平切线来找函数最大值和最小值的方法与今天微积分的求解方法极其相仿,因此拉格朗日甚至称费马才是“微积分之父”。更早之前甚至可以追溯到公元前7世纪,古希腊科学家泰勒斯就对球的面积、体积、与长度等问题的研究就含有微积分思想。阿基米德在研究解决抛物线下的弓形面积、球和球冠面积、螺线下的面积和旋转双曲线所得的体积的问题中也隐含着近代积分的思想。三国时期的刘徽所研究的割圆术对积分学也有研究。遗憾的是,在微积分发展最为迅速的中世纪,我国正处于闭关锁国的明清时代,没能与世界上其他的数学家一起狂欢。

莱布尼兹画像
在当时,牛顿和莱布尼兹发明微积分还引起了一场轩然大波,英国皇家学院支持本土的牛顿,而另外一些欧洲大陆的国家则推崇德国的布莱尼茨,这一对抗竟然绵延了一个世纪之久,导致了微积分发展的停滞。事实上,牛顿和莱布尼茨分别是自己独立研究,并且有意思的是两个人也是在相近的时间里先后完成自己的研究。牛顿创立微积分要比莱布尼茨早10年左右,但是莱布尼茨正式公开发表微积分这一理论却要比牛顿早三年。时间的先后并不能说明多少问题,而且他们虽然都是研究微积分,但研究方向其实并不相同,牛顿在1671年写了《流数术和无穷级数》,指出变量是由点、线、面的连续运动产生的。他在流数术中所提出的中心问题是:已知连续运动的路径,求给定时刻的速度,或已知运动的速度求给定时间内经过的路程。莱布尼茨在1684年发表了现在世界上认为是最早的微积分文献。这篇文章的题目相当抢眼,叫做《一种求极大极小和切线的新方法,它也适用于分式和无理量,以及这种新方法的奇妙类型的计算》。这篇看上去有些潦草的文章却包含了现代的微分符号和基本微分法则。1686年,莱布尼茨发表了第一篇关于积分学的文献。现今我们使用的微积分通用符号就是当时莱布尼茨所选择的。简单来说,牛顿研究微积分着重于从运动学来考虑,莱布尼茨却是侧重于几何学来考虑的。他们的最大功绩是把两个貌似毫不相关的问题联系在一起:一个是切线问题——微分学的中心问题,一个是求积问题——积分学的中心问题。
微积分的英文是Calculus,这并非英语,而是拉丁语,原义是小石头。看到这里,可能很多人都不明白了,到底是谁要用这样一个平实普通的事物来为命名如此高大上的一门新兴学科?答案就是莱布尼茨。在古时候,人们会使用小石头作为计算工具,久而久之,小石头就代表了一种计算方式。因此莱布尼茨很巧妙地采用这一传统的称呼来为新兴事物命名。另外,莱布尼茨还用拉长的S来表示积分,用d来代表差,这两个单词也都是从拉丁语中化来。而牛顿则创造出Fluxion(通量)这个名词来表示导数。并且发现了第一个版本的微积分定理。所以很难说两个人谁对微积分发明的贡献更大。现在,人们普遍认为是牛顿、莱布尼茨两人分别建立起各自的体系,没有互相交流,更不存在抄袭这样的恶劣问题。笔者这是一种非常正确和健康的学术心态,与其去纠结这样难以查明的历史遗留问题,不如多做一些科学研究为明天的数学大厦建设增砖添瓦。这才是每个学者应该关心的问题。
很多人不学习数学,也不了解数学,但是不得不承认,微积分真的有用,我们生活的物质世界就是由这样的理论支撑才得以建立。

 更多
更多
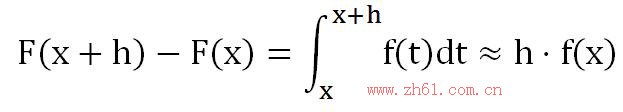
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底