第4 章连续性和可导性

来看看函数的两种类型的光滑性: 连续性和可导性.
5.1 连续性
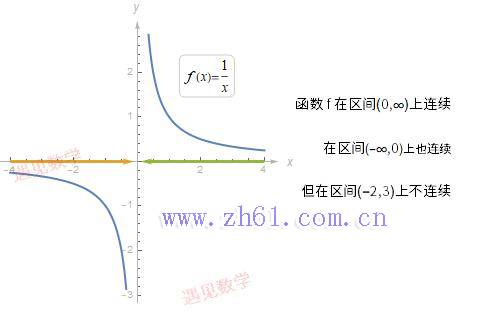
比如对于 y=1xy=1x 这样的函数在 x=0 处有一条垂直渐近线, 把函数图像分成了两部分.
5.1.1 在一点处连续
5.1.2 在一个区间上连续
清楚了函数在一个单点上连续的定义, 再看函数在区间 (a,b) 上的每一点都连续, 那么它在该区间上连续.
对于形如 [a, b] 的区间, 这里对于点 x=a 和 b 需要函数的单侧连续性.
5.1.3 连续函数的一些例子
很多的常见函数都是连续的. 例如, 每一个多项式都是连续的(证明见书)
5.1.4 介值定理
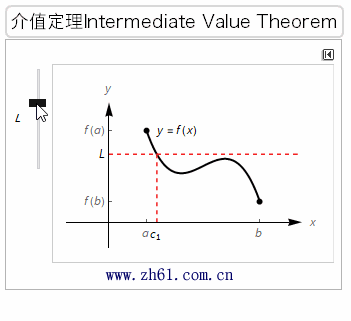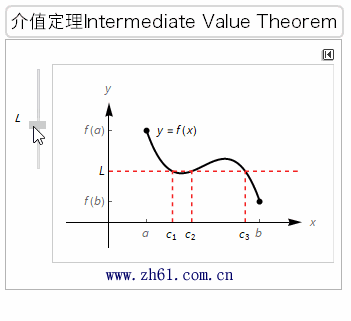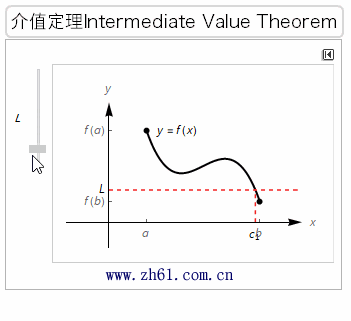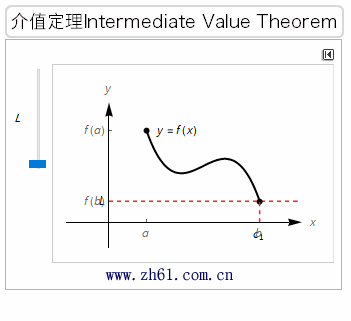
知道一个函数是连续的会有很多好处. 我们将看看其中两个好处. 第一个介值定理(intermediate value theorem)就是用到了连续函数在两点之间的连续性.
书中给出的介值定理其实是零点定理, 如下所示:
5.1.6 连续函数的最大值和最小值
数是连续的所带来的第二个好处给出了最大值和最小值定理:
5.2 可导性
连续性意味着函数光滑, 另一种表示光滑的特性就是可导性, 这实质上就表示函数有导数. 发展微积分的最初灵感之一来自试图去理解运动物体的速度、距离和时间的关系.
5.2.1 平均速率(Average speed)
位移= 终点位置 - 初始位置.
速度可以是负的, 而速率必定是非负的.
5.2.3 瞬时速度(Instantaneous velocity)
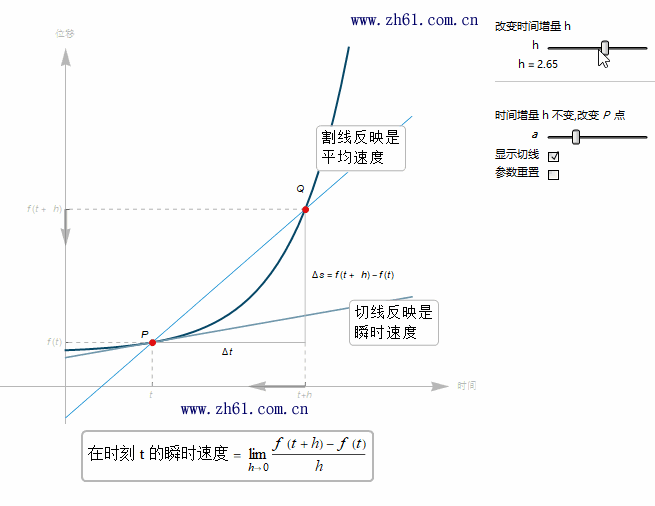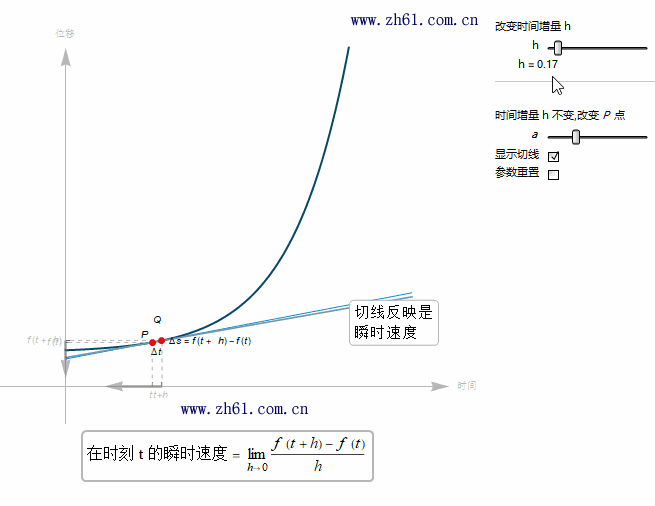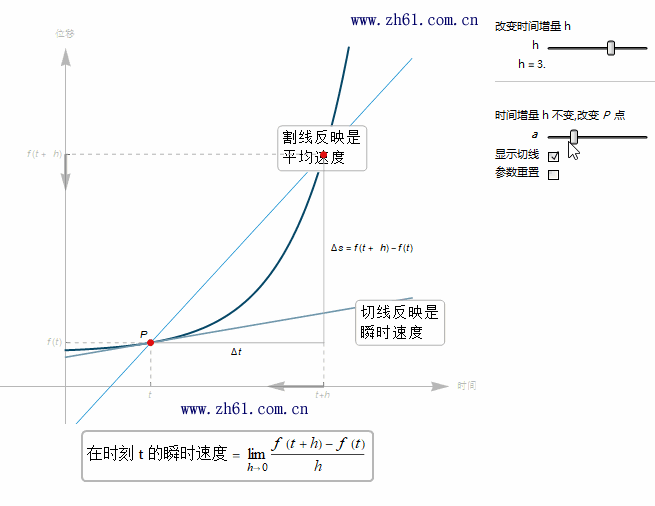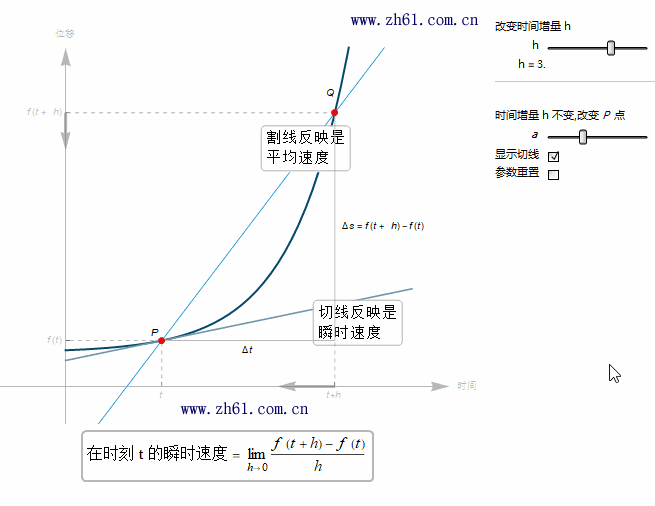
5.2.4 速度的图像阐释(The graphical interpretation of velocity)
当 t+h 趋于 t 时, Q 点就越来越接近点 P 点. 由于瞬时速度是割线在 h 趋于 0 时的极限. 于是瞬时速度就等于通过点 P 的切线的斜率.
5.2.5 切线(Tangent lines)
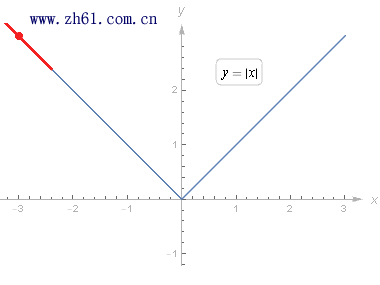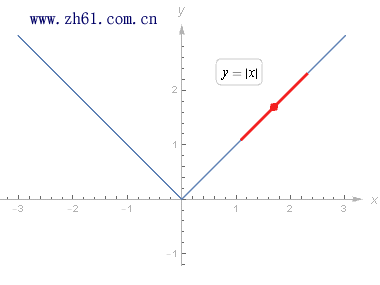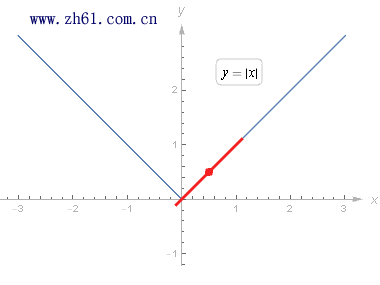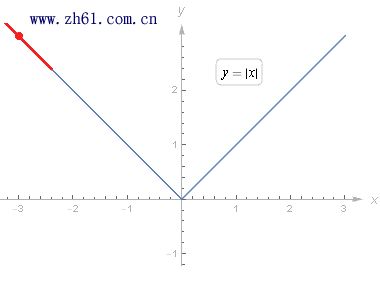
首先需要注意的一点, 可能在一个图像上给定的一点没有切线. 例如, 考虑 y = |x| 的图像, 在 (0,0) 处没有切线, 因为原点处是尖点, 不能在那里同时顾及两边的图像.
如果通过(x, f (x)) 的切线存在, 你又该如何找到它?
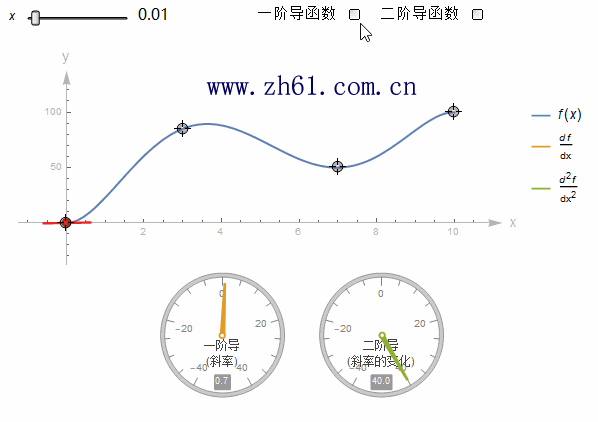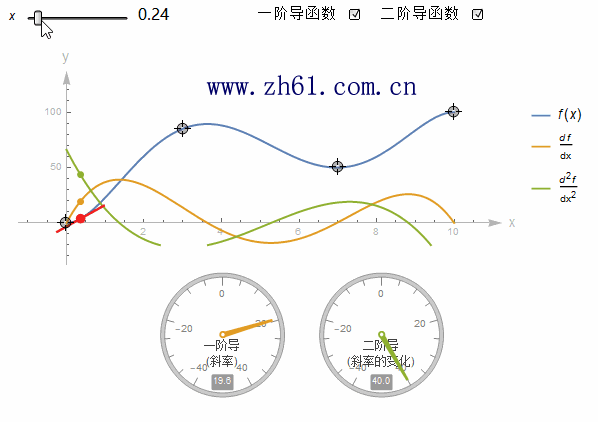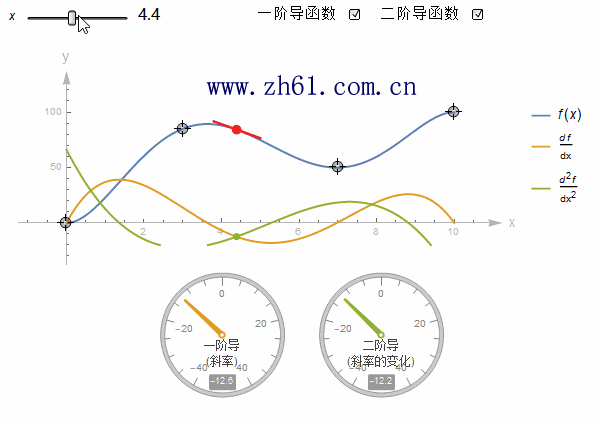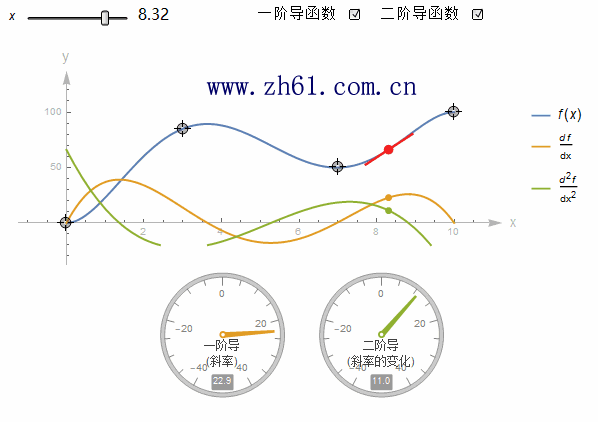
5.2.6 导函数
对f 关于变量x 求导得到函数 f' , 也即是
如果对于某个特定的 x, 极限不存在, 那么x 的值就没有在导函数 f' 的定义域里, 即 f 在 x 点不可导.
5.2.7 作为极限比的导数
在导函数 f' (x) 的公式中, f (x + h) - f(x) 其实为 y 的增量.
该公式的一个阐释是, x 中的一个小的变化产生了大约 f' (x) 倍的 y 中的变化. 用 dx 表示x 中的十分微小的变化". 对y 也有类似的表示方法, 可以用一种不同的且更方便的方法来写导数:用 dydxdxdy来代替 f'(x).
5.2.9 二阶导数和更高阶导数
函数 f 取其导数得到一个新的函数 f', 实际上可以采用这个新的函数, 再次求导. 最终得到导数的导数, 这被称为二阶导, 写作 f'', 可以用 d2ydx2d2ydx2来代替.
5.2.10 何时导数不存在
右导数和左导数的思想定义分别为:
跟在极限的情况一样, 如果左导数和右导数存在且相等, 那么实际的导数存在且有相同的值. 同时, 如果导数存在, 那么左右导数都存在且都等于导数值.
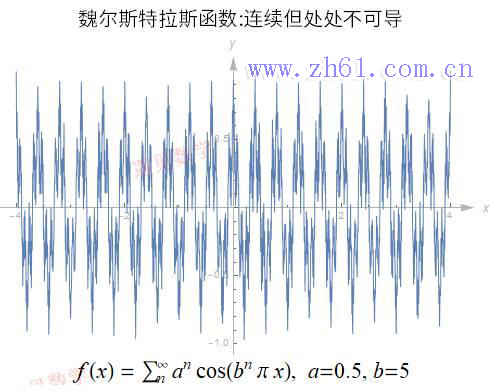
函数 |x| 就是在其定义域内不是处处可导的连续函数, 不过除了 x=0 点外函数可导. 也存在着连续但处处不可导的函数, 如下面所示的魏尔斯特拉斯函数.
5.2.11 可导性和连续性(Differentiability and Continuity)
可导函数必连续. 不过从上面 |x| 例子, 就可以知道连续函数并不总是可导的!
(本章完)

 更多
更多



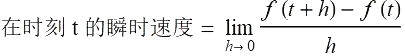

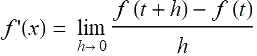

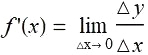
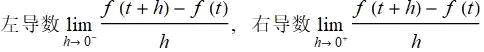
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底