[遇见数学] 基于风靡美国《普林斯顿微积分读本》一书所制作图解系列, 内容章节安排完全按照此书推进, 提供更多的图像和动画来让读者体会微积分的无穷魅力, 建议配合原书来学习. 关注 [遇见数学] 收看更多图解课程!

第 8 章 隐函数求导和相关变化率

隐函数的求导是对常规求导的一般化, 如果知道一个量的变化有多快, 我们就能求出另一个不同的但与之相关的量的变化会有多块.

8.1 隐函数求导(Implicit Differentiation)

考虑两个导数 d(x^2)/dx 和 d(y^2)/dx .

第一个就是问当对 x 稍作改变时候, 量 x^2 会有多大的变化(会有近似 2x 倍那么多的变化).

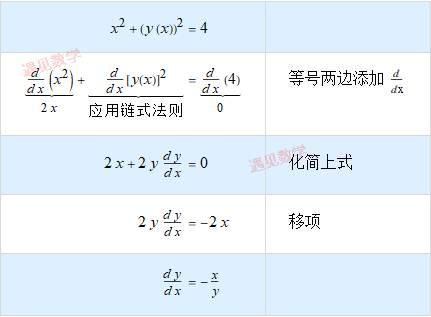
第二个 y 是依赖与 x 的. 可以这样思考: 如果改变了 x , 那么 y 就会有变化. y 这种变化又会引起 y^2的变化. 这样根据链式求导法则:

因此, 当 x 有少许的改变, 那么 y^2 就有 2y dy/dx 倍的变化.

8.1.1 技巧和例子

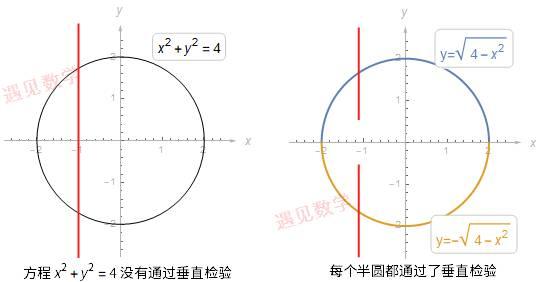
考虑方程 x^2+y^2=4 , 图像就是半径为2、圆心位于原点的单位圆.

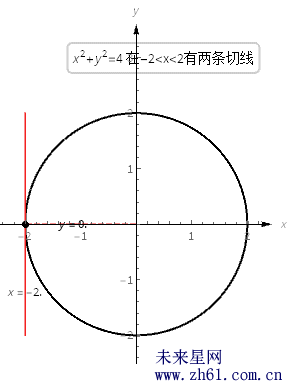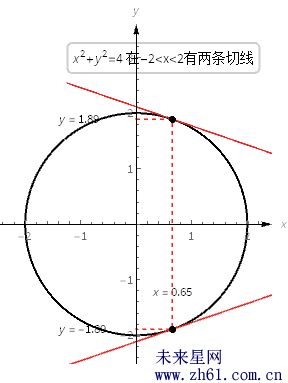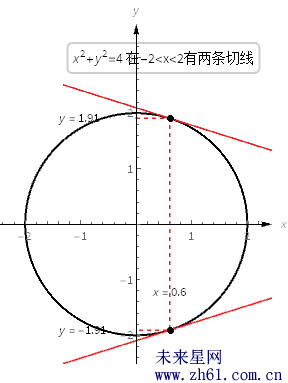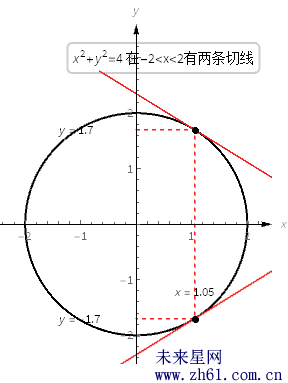
这个公式说的是, 圆上点(x, y) 处的切线的斜率是 −x/y.

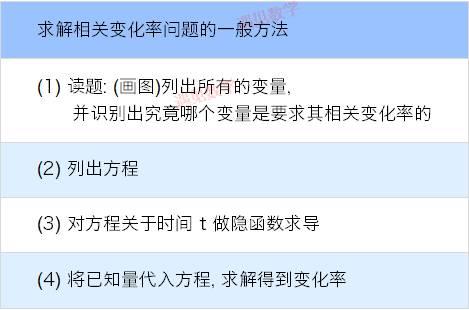
8.2 相关变化率(Related Rates)

定义 :变化率是一个量随时间改变的速率. 也就是说 - 如果 Q 是某个量, 那么 Q 的变化率是 dQdtdQdt.

当你看到"变化率"这几个字的时候, 就应该自动想到 d/dt .

8.2.1 一个简单的例子

下面是一个说明上述方法的相对简单的例子. 设想用打气筒给一个完美球体的气球充气. 空气以常数变化率 12 π 立方英寸每秒进入气球. 当气球的半径达到2 英寸时, 气球的半径的变化率是多少？此外, 当气球的体积达到 36 π 立方英寸时,气球的半径的变化率又是多少？

也就是说如果我们知道半径 r , 那么就可以求出半径的变化率 3r23r2.

8.2.2 一个稍难的例子

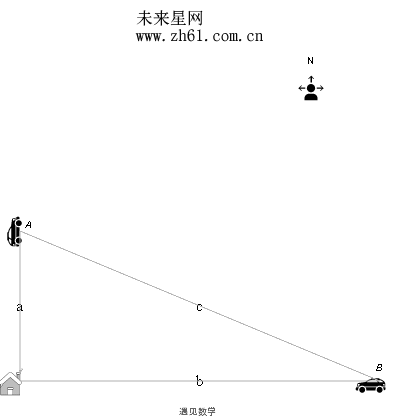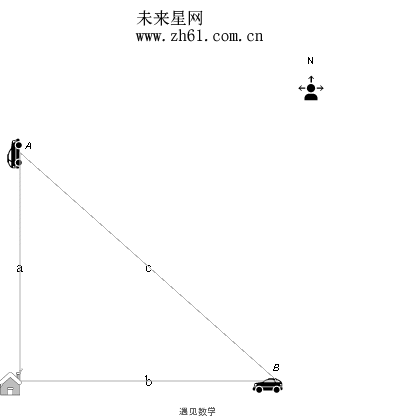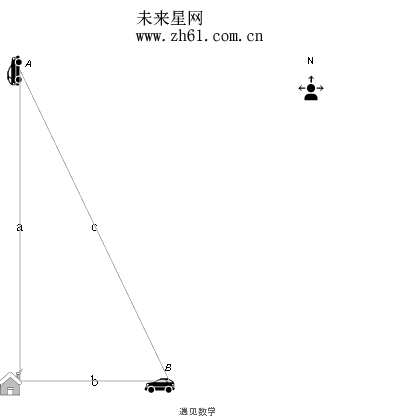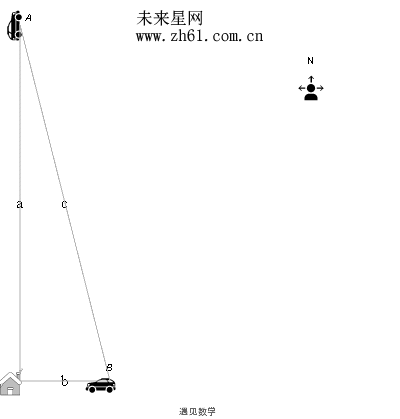
有两辆汽车 A 和 B. 汽车A 在一条路上径直向北行驶远离你家, 而汽车 B 在另一条路上径直向西行驶接近你家. 汽车A 以55 英里/小时的速度行驶, 而汽车 B 以45 英里/小时的速度行驶. 当A 到达你家北面21 英里, 而B 到达你家东面28 英里时, 两辆汽车间的距离的变化率是多少？

先来看下动画演示, 作为解题的第一步骤.

更多例子请查看书中的示例

(本章完)

「予人玫瑰, 手留余香」

转发既是支持和帮助, 感谢感谢!