微积分是数学中的一门重要分支,它涉及到函数、极限、导数、积分、微分方程等多个概念,在工程、科学、经济等领域都有广泛的应用。微积分分为五个主要的章节:导数与微分、积分与定积分、微分方程与应用、多元函数与偏导数、向量函数与曲线积分。本文将逐一介绍这些内容,以帮助读者了解微积分的基础理论和实际应用。
一、导数与微分
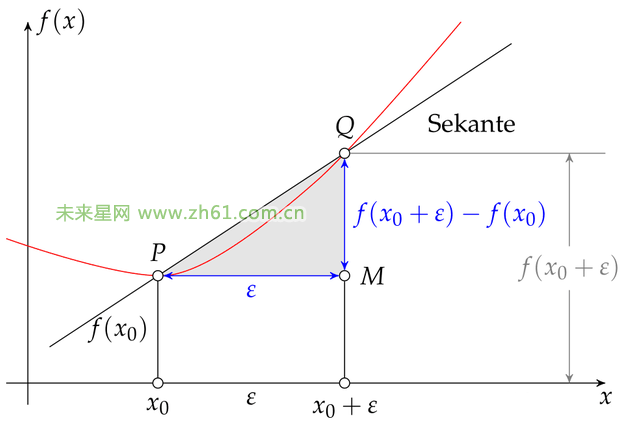
导数和微分是微积分理论的基础,它们可以用来描述曲线的变化率、切线斜率以及局部增长和减少的趋势等。导数是函数在某一点的变化率,用极限的概念表示;微分是函数在某一点的切线的近似值,用微分算子的形式表示。导数和微分是密切相关的,在求解导数的同时,也可以求出函数在某一点的微分值。
以函数 f(x) = x^2 为例,其导数的计算公式为:
在微积分中,由于极限的存在性,我们可以通过逐步缩小 △x 的值,从而求得 f(x) 在某一点的导数值。此外,微分也是导数的一种几何意义,它表示函数在某一点的切线斜率,可以用于研究函数的局部特征。
二、积分与定积分
积分是微积分理论的另一个重要分支,它可以用来计算曲线下方的面积、弧长、体积以及质心等。积分分为不定积分和定积分,其中不定积分表示函数的原函数,而定积分则用于求解函数在一段区间内的积分值。
以函数 f(x) = x^2 为例,其不定积分的计算公式为:
其中 C 为常数。而定积分的计算公式为:
表示函数 f(x) 在区间 [a, b] 内的积分值,可以用定积分公式计算得出。
在实际应用中,积分经常用于求解曲线下方的面积、不规则图形的面积、物体的质心以及流体的体积等问题。同时,定积分也被广泛应用于金融领域,例如计算复利和现值等问题。
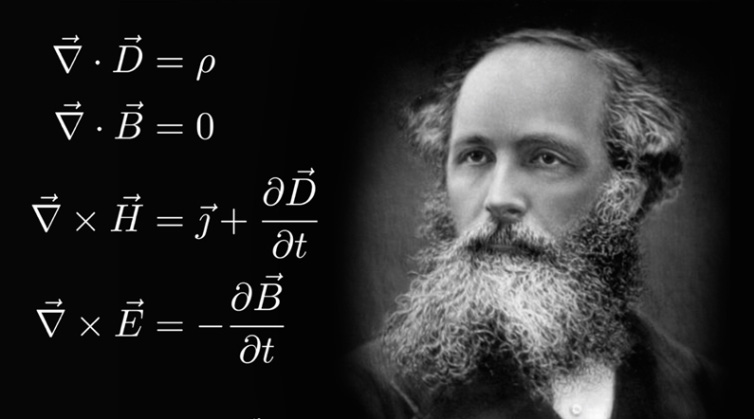
微积分的应用,麦克斯韦方程组
三、微分方程与应用
微分方程是微积分理论中的一个重要分支,它可以用来描述各种物理现象、化学反应、生物进化以及各种经济模型等。微分方程分为常微分方程和偏微分方程,前者描述的是只涉及一个自变量的函数,后者描述的是涉及多个自变量的函数。
以一阶常微分方程 y' + y = cos x 为例,其求解过程如下:
首先将方程改写成标准形式: y' = -y + cos x ,然后求解其通解:
其中 C 为常数。此外,我们还可以通过初值条件求解微分方程,即通过已知的初始值求解出特定的解。
微分方程的应用十分广泛,例如可以用来描述弹簧振动、电路的变化、生物中的肿瘤扩散、经济模型的预测等。通过求解微分方程的解析解或数值解,我们可以更好地理解各种自然现象和工程问题,并为解决复杂问题提供有效的数学方法。
四、多元函数与偏导数
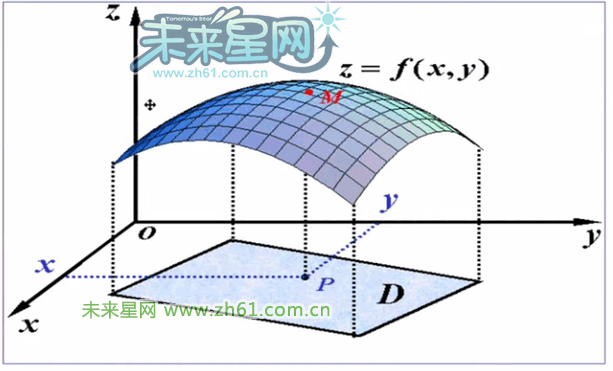
多元函数和偏导数是微积分理论中重要的扩展内容,它们可以用来描述多维空间中的曲面和曲线的性质,以及分析各种复杂问题。在多元函数中,自变量不再是单个变量 x,而是包含多个变量的向量,例如 (x,y,z)。
以二元函数 z = x^2 + y^2 为例,其偏导数的计算公式为:
其中,第一个式子表示 z 对 x 的偏导数,第二个式子表示 z 对 y 的偏导数。偏导数可以用于研究函数在多维空间中的局部性质,例如曲面的切平面、极值点等。
此外,在实际应用中,多元函数和偏导数还可以用于描述电场、磁场、流体力学等复杂现象,在金融领域中也可以利用多元函数和偏导数来进行资产组合优化、风险分析等方面的决策支持。
五、向量函数与曲线积分
向量函数和曲线积分是微积分中比较高阶的内容,它们可以用来描述三维空间中的曲线和表面的性质,以及分析各种流体力学、电磁学和物理学问题等。向量函数描述的是在空间中的一个运动路径,其自变量是时间 t 。
以向量函数
为例,其弧长和曲线积分的计算公式为:
其中 ds 表示弧长,F 表示向量场,
表示向量场 F 沿着曲线 C 的曲线积分值。
向量函数和曲线积分的应用非常广泛,例如可以用来描述质点的运动、电场、磁场、流体力学等复杂现象;在机器人控制、计算机图形学和三维计算机动画等领域中,向量函数和曲线积分也扮演着重要的角色。
总结
微积分是数学中非常重要的一门学科,涉及到导数、积分、微分方程、多元函数以及向量函数等多个概念。通过深入学习微积分理论,我们可以更好地理解和掌握各种自然现象和工程问题,并为解决复杂问题提供有效的数学方法。同时,在实际应用中,微积分也被广泛应用于物理学、化学、生物学、经济学以及计算机科学等多个领域,具有十分广泛的应用前景。

 更多
更多

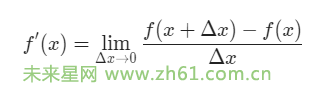

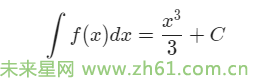
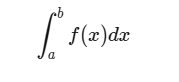





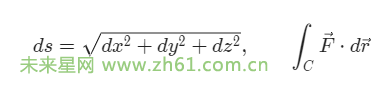
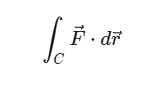
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底