第10 章反函数和反三角函数
这一章主要内容:
-
使用导数证明一个函数有反函数;
-
求反函数的导数;
-
逐个来看反三角函数;
-
反双曲函数.
10.1 导数和反函数
第一章就回顾了反函数的基本知识, 可以快速地再看下. 现在讨论导数和反函数之间的两个联系.
10.1 .1 使用导数证明反函数存在
如果一个可导函数 f , 它的导数总是正的, 那么该函数一定是递增函数, 且满足水平线检验(如不清楚, 请查看第一章内容, 跳转链接>>>). 没有水平线会与 y = f (x) 相交两次. 由于 f 满足水平线检验, 所以我们知道 f 有反函数.
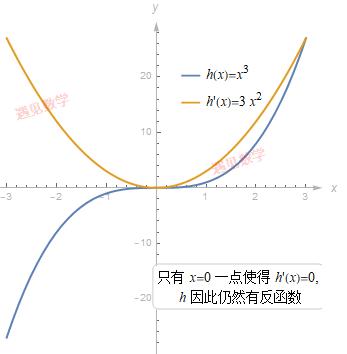
函数上只有一个点使得 h'(x)=0, 这样仍然有反函数.
10.1.2 导数和反函数:可能出现的问题
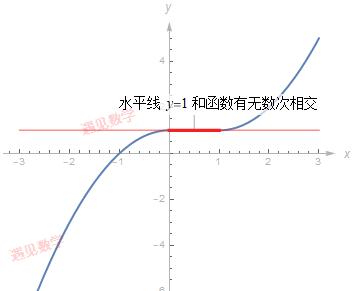
函数的导数可以偶尔是0, 而该函数仍然有反函数. 但下图中函数没有通过水平检验, 在 y=1 和该函数有无数次相交(红色线段标识出), 故不存在反函数.
一般来说当函数有不连续点或垂直渐近线时, 上面导数和反函数的方法也不再适用了.
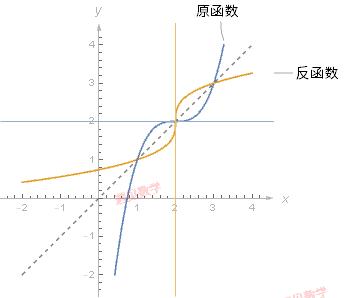
10.1.3 求反函数的导数
知道函数 f 有反函数, 我们通常称之为 f−1f−1, 该反函数的导数就是原函数的导数的倒数.
如果一个函数, 它有反函数, 并且原函数在点 (x,y) 处的斜率为0, 则其反函数在点(y, x) 处的斜率将会是无限的.
10.2 反三角函数
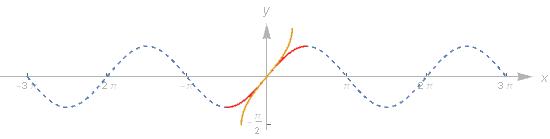
将 sin(x) 定义域限制为区间 [-π/2, π/2], 则它满足水平线检验, 故它有反函数 f−1f−1, 写成 sin−1(x)sin−1(x) 或 arcsin(x) .
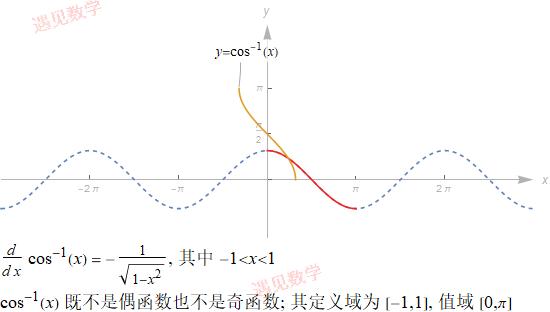
10.2.2 反余弦函数
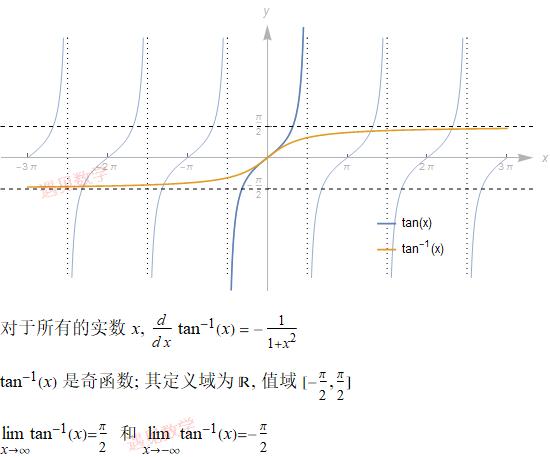
10.2.3 反正切函数
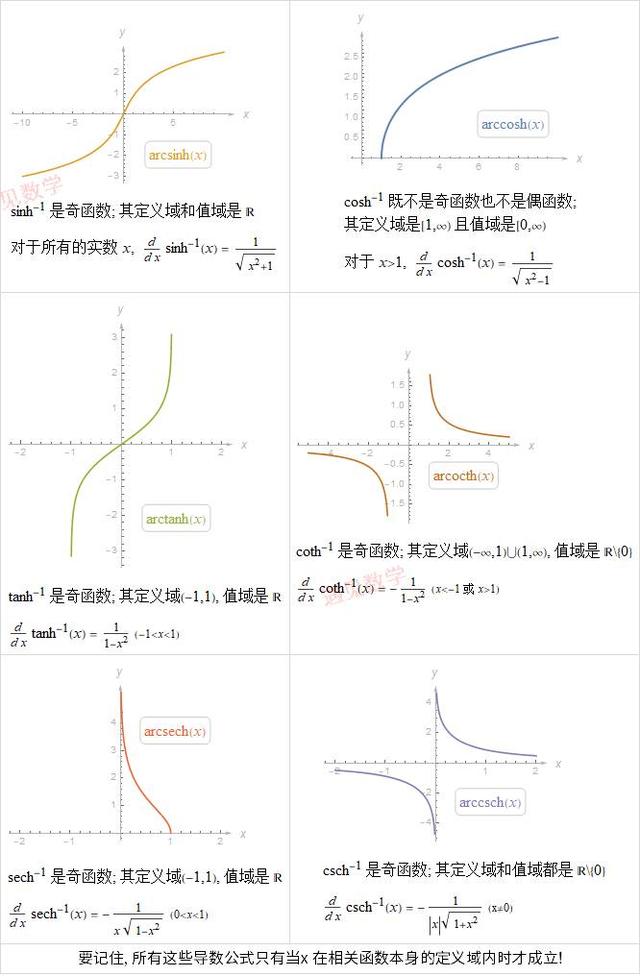
10.3 反双曲函数
要记住, 所有这些导数公式只有当 x 在相关函数本身的定义域内时才成立!
(本章完)
「予人玫瑰, 手留余香」
转发既是支持帮助[遇见数学]更快发展, 非常感谢!

 更多
更多
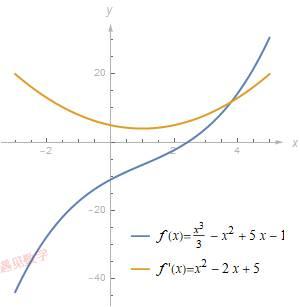

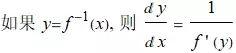

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底