微积分(Calculus)是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。是数学的一个基础学科。
微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。
积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法。
目录
1 函数与自变量的关系
函数,从字面理解就是包含自变量,与自变量有对应关系的变量。
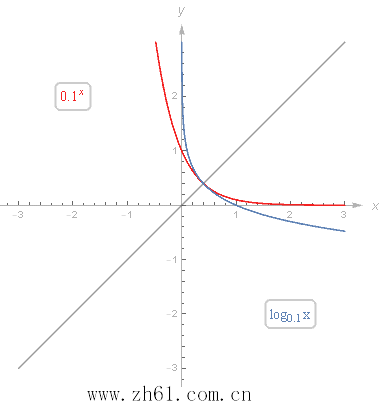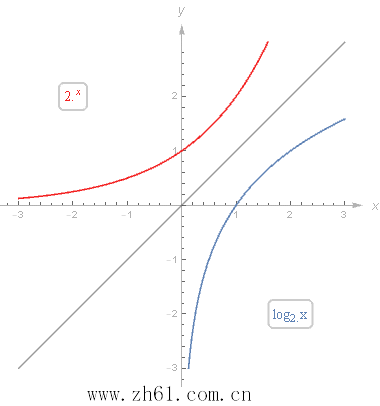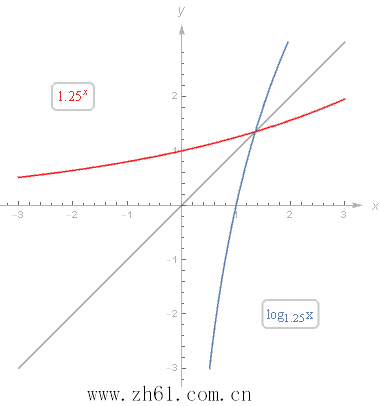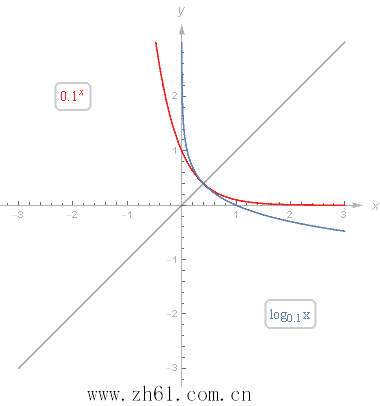
2 对数函数与指数函数的关系
对数函数与指数函数互为反函数。
3 自然常数e
e 是描述增长率的自然常量, 并且 e^x 还是唯一具有下面性质的函数:
这个函数曲线上的每一个点的 y 值, 在该点的斜率和曲线下面积三者都是相同值.
特别是当 x =1 时, 函数值就等于 e. 斜率也是 e, 而曲线下的面积也是 e.
也正是因为这个主要性质, 使得它成为了微积分中最喜闻乐见的符号(微积分也正是描述变化率, 极限求和的数学). 所以当在微积分课程中, 每每遇到 e 的计算, 你觉得计算应该会简单很多.
4 单位弧度
单位弧度:圆弧长度等于半径时对应的圆心角。
5 一个完整的圆的弧度
一周的弧度数为2πr/r=2π,360°角=2π弧度,因此,1弧度约为57.3°,即57°17'44.806'',1°为π/180弧度,近似值为0.01745弧度,周角为2π弧度,平角(即180°角)为π弧度,直角为π/2弧度。在具体计算中,角度以弧度给出时,通常不写弧度单位,直接写值。下面是是一些常用角的度和弧度表达.
6 介值定理
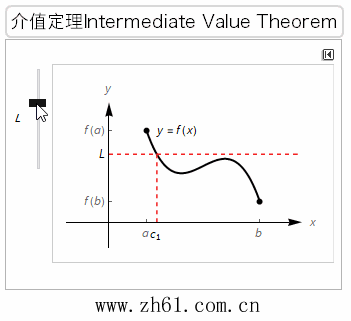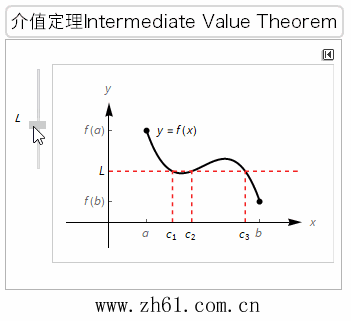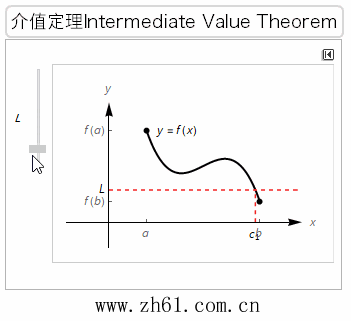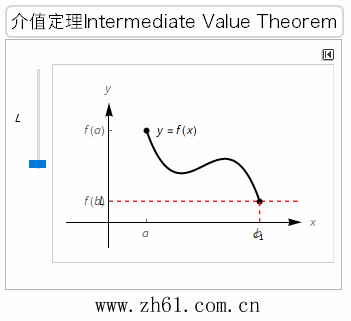
介值定理,又名中间值定理,是闭区间连续函数的重要性质之一。在数学分析中,介值定理表明,如果定义域为[a,b]的连续函数f,那么在区间内的某个点,它可以在f(a)和f(b)之间取任何值,也就是说,介值定理是在连续函数的一个区间内的函数值肯定介于最大值和最小值之间。
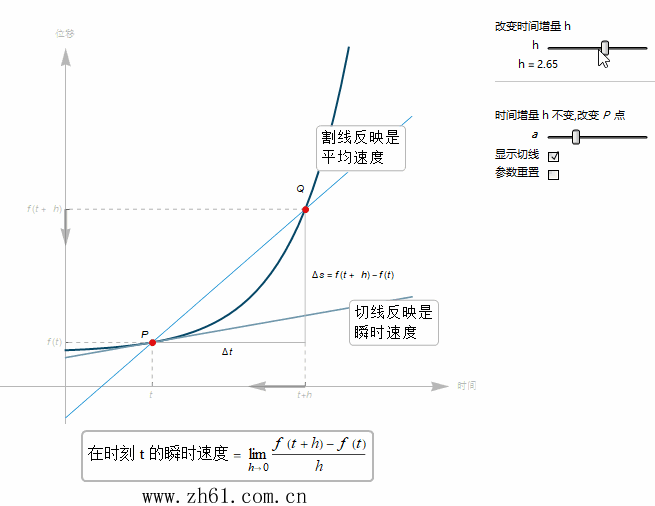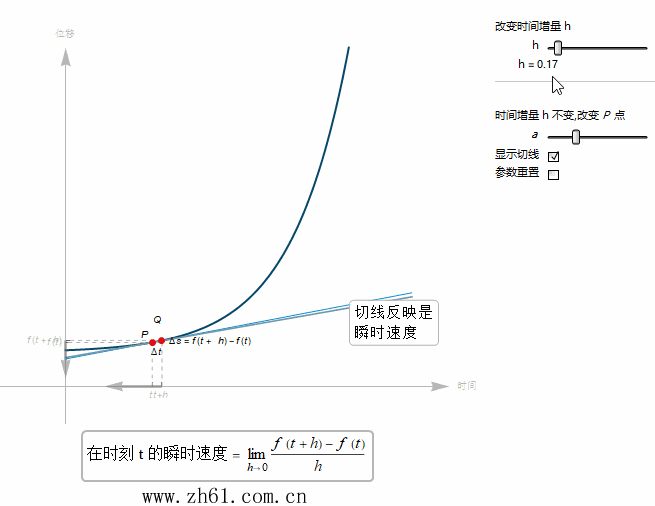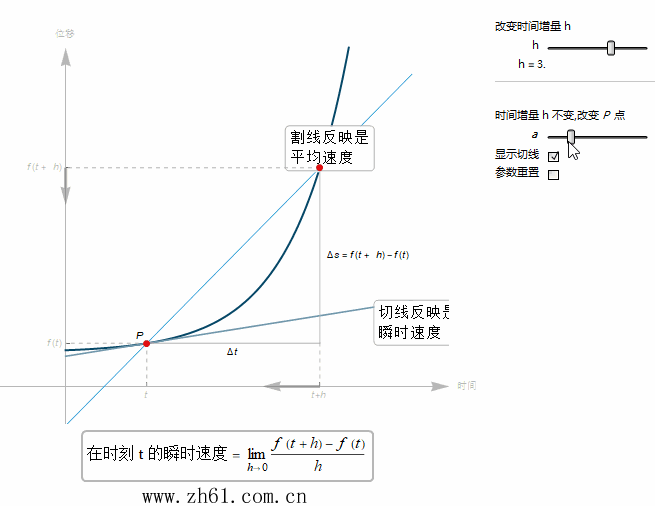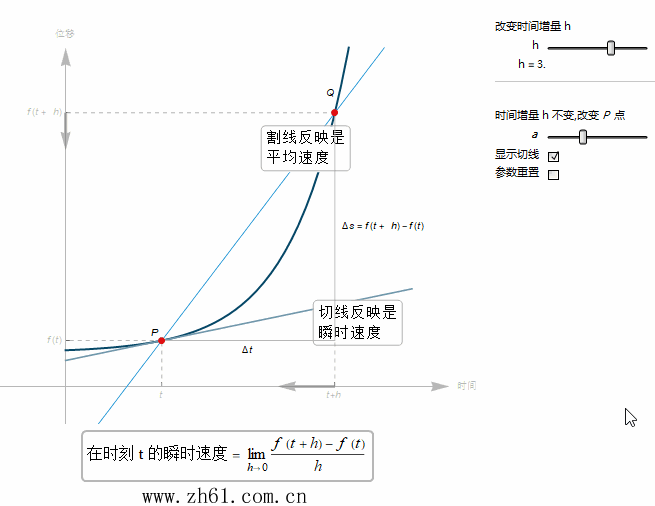
7 速度的图像阐释
当 t+h 趋于 t 时, Q 点就越来越接近点 P 点. 由于瞬时速度是割线在 h 趋于 0 时的极限. 于是瞬时速度就等于通过点 P 的切线的斜率.
7 导函数
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
对f 关于变量x求导得到函数 f' , 也即是
8 二阶导数和更高阶导数
函数 f 取其导数得到一个新的函数 f', 实际上可以采用这个新的函数, 再次求导. 最终得到导数的导数, 这被称为二阶导, 写作 f''.
9 切线方程
求导的一个好处就是可以使用导数来求所给曲线的切线方程. 求出过该点的切线的斜率是 f' (x), 使用点斜式来得到切线方程.
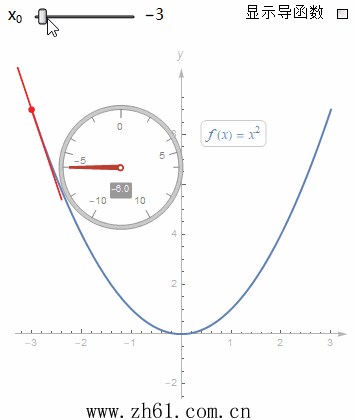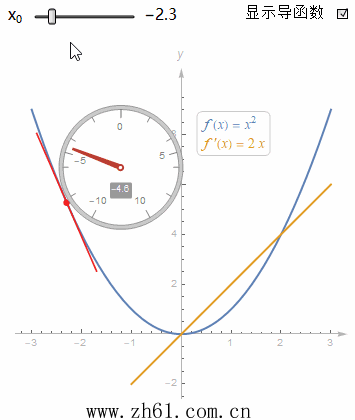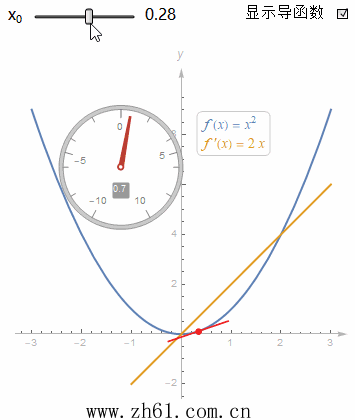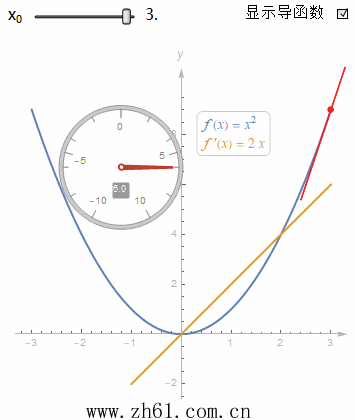
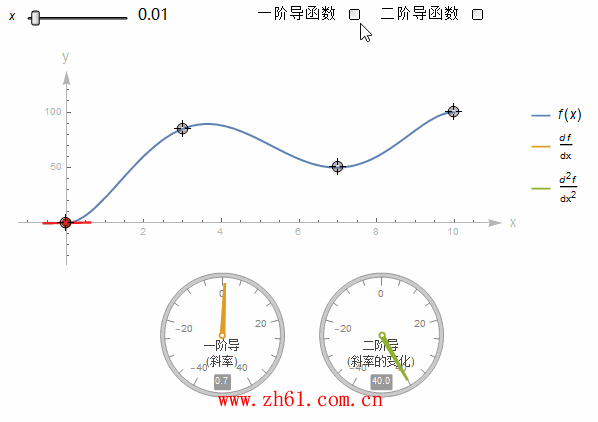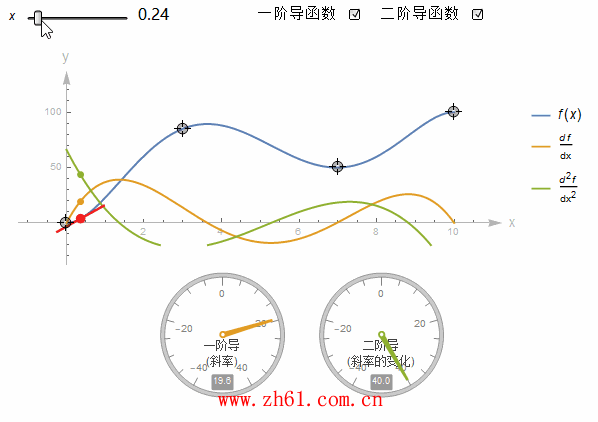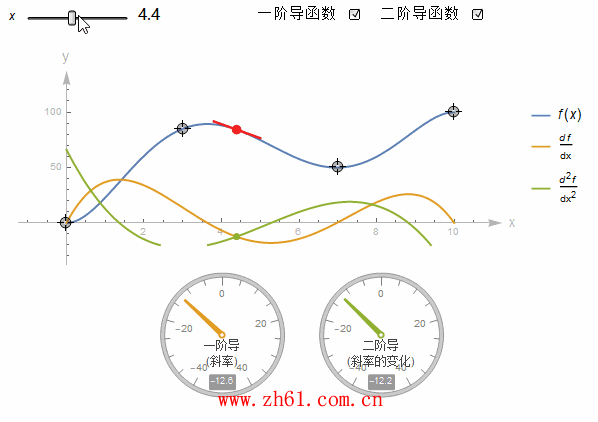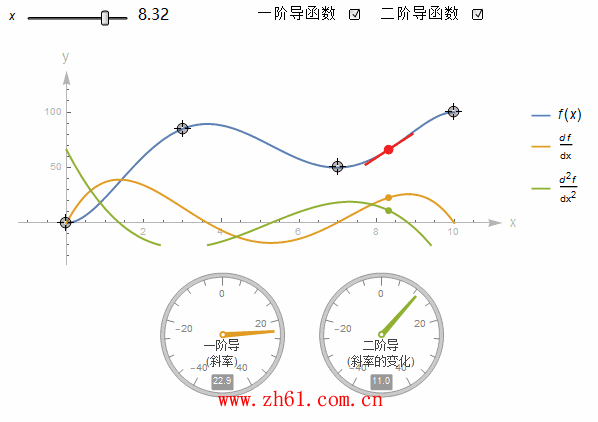
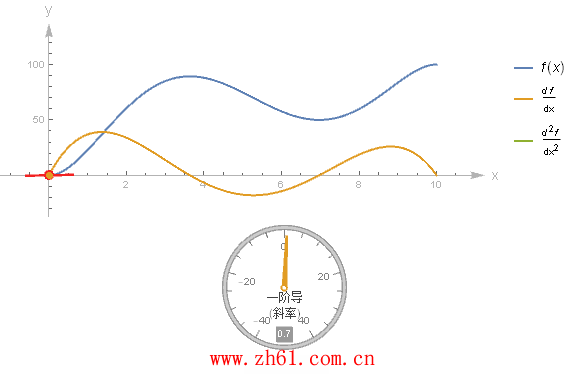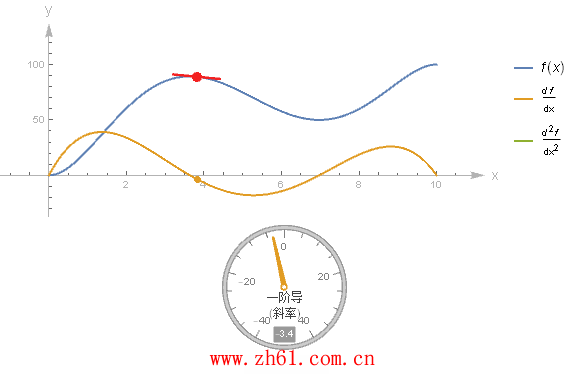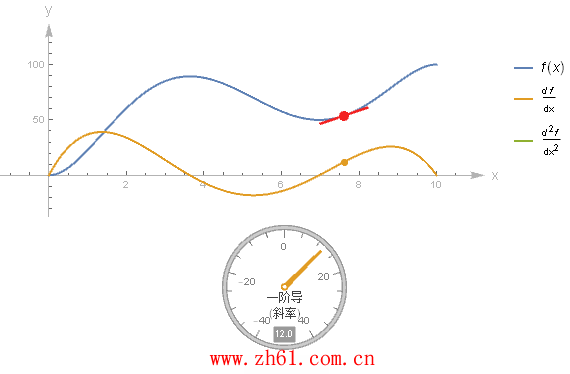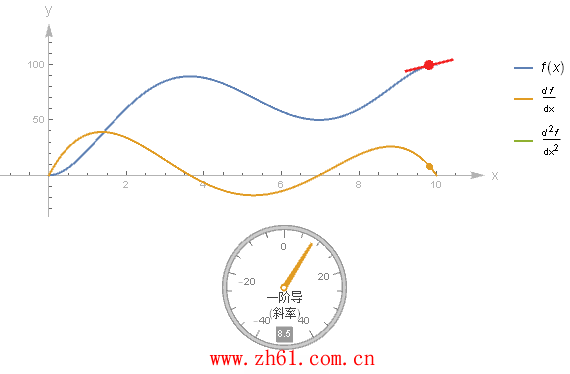
10 直接画出导函数的图像
假设有一个函数的图像, 你不知道它的方程, 但又想要画出其导函数的图像, 这就需要你对微分有一个很好的理解. 这里制作一个动图来加深对导函数的印象.
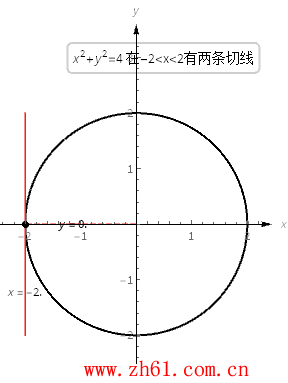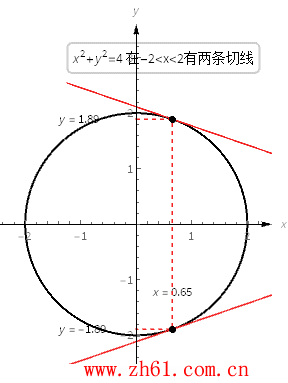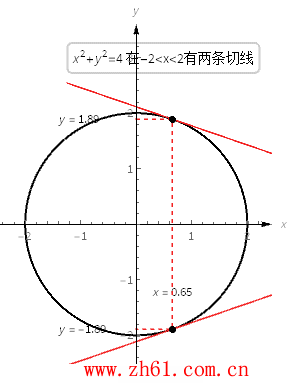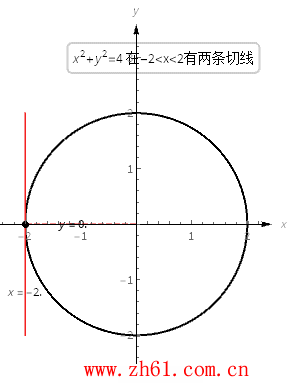
11 单位圆的切线斜率
考虑方程 x^2+y^2=4 , 图像就是半径为2、圆心位于原点的单位圆.
圆上点(x, y) 处的切线的斜率是 −x/y.
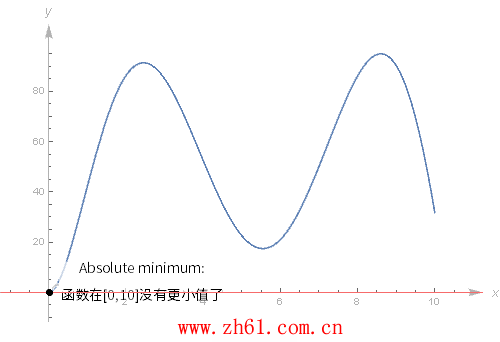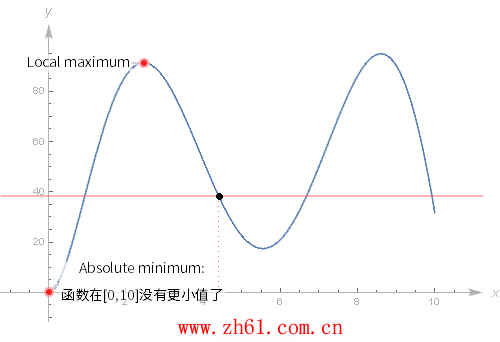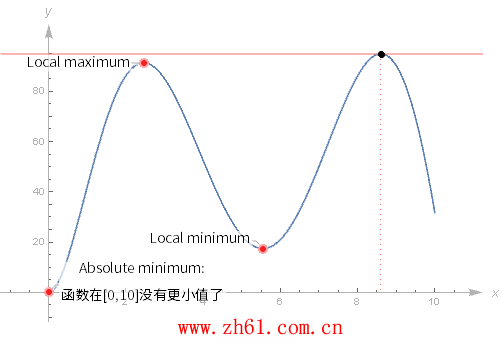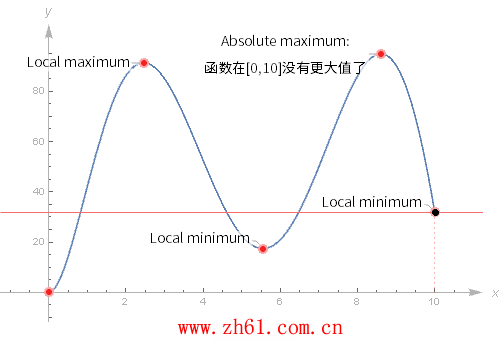
12 全局极值和局部极值
通过函数的导数可以找到函数的极值。
13 罗尔定理
罗尔定理(Rolle's Theorem)假设函数 f 在闭区间 [a,b] 内连续, 在开区间 (a, b) 内可导. 如果 f(a) = f(b); 那么在开区间 (a,b) 内至少存在一点 c, 使得 f'(c) = 0.
14 中值定理(Mean Value Theorem)
中值定理:假设函数 f 在闭区间 [a,b] 内连续, 在开区间 (a,b) 内可导, 那么在开区间 (a,b) 内至少有一点 c 使得 f(b)−f(a)b−a=f'(c)f(b)−f(a)b−a=f'(c).
中值定理和罗尔定理这两个定理的条件几乎是相同的. 在两个定理中, 函数f 都要求在闭区间 [a,b] 内连续, 在开区间 (a,b) 内可导. 但罗尔定理还要求 f(a) = f(b), 中值定理则没要求这一点.
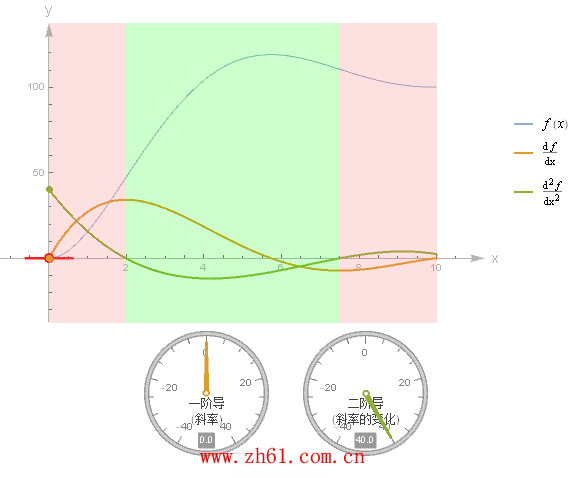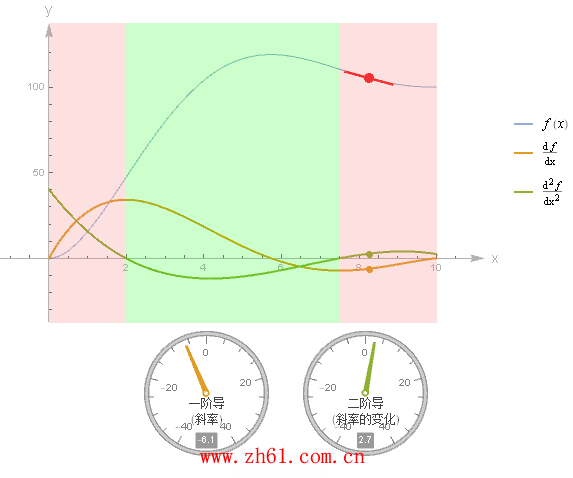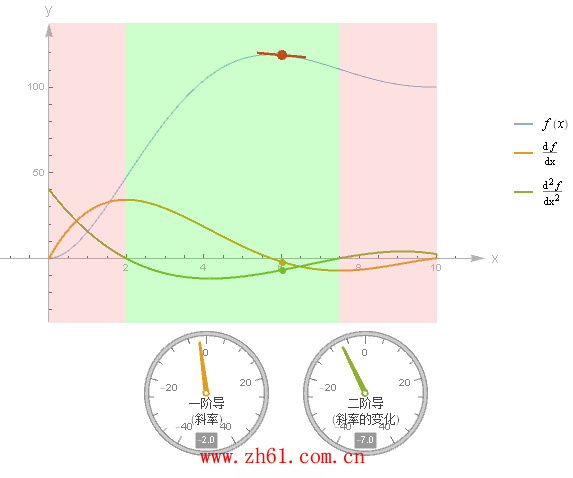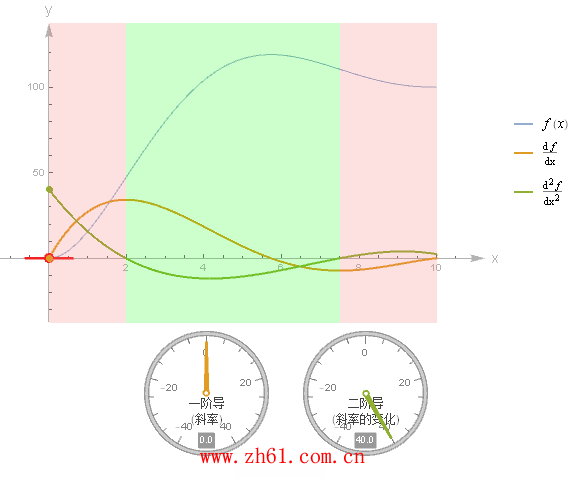
15 二阶导数和图像
如果把二阶导数看作导数的导数, 那么可以把二阶导数写为 (f')'(x) > 0. 这意味着导函数 f'(x) 始终是增函数.
观察下面图中不同的 (0,2) 与 (7.5, 10)范围二阶导数 f''(x) > 0 (凹向上, 如碗型: 凸函数Convex function), 所以导函数 f'(x) 始终是增函数;而在 (2,7.5) 区间二阶导数 f''(x) < 0(凹向下:="" 凹函数concave="" function),="" 所以导函数="" f'(x)="">
原函数凹凸性改变的地方,称之为拐点(inflection point), 也是上图区域颜色改变之处(用红点标识出来的地方).
16 一个最优化的例子
假设只有300 英尺长的篱笆可供使用, 并且农场主想要围成一个直角三角形的农场, 并且使新圈出的地的面积(下图绿色三角形区域)尽可能地大. 那么这块地的周长和面积分别为多少?
(1) 首先要识别出一些变量. 设三角形的底边为 b, 高为 h, 斜边为H, 并且面积 A. 限制条件篱笆的长度 h+H, 目标最大化 A;
(2) 由题意可知 0<><=300,><><=300,><><>
(3) 列出方程组 A=bh/2, h+H=300, b^2+h^2=H^2;
(4) 消去 b 和 H 得到 A 的方程;
(5) 求导 dA/dh=45(100−h)√900−6h
(6) 求得 h=100 时候, A = 5000√3, 并进行验证
(7) 得到结论.
17 微分(The differential)
微分概念是在解决直与曲的矛盾中产生的,其中心思想是无穷分割。
设函数y = f(x)在x的邻域内有定义,x及x + Δx在此区间内。函数的增量可表示为Δy = f(x + Δx) - f(x)。
通常把自变量x的增量 Δx称为自变量的微分,记作dx,即dx = Δx。于是函数y = f(x)的微分又可记作dy = f'(x)dx。函数的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。
f(x + Δx) - f(x)= f'(x)dx
当x=a时,则f(a + Δx)= f(a)+f'(a)Δx
量df 被称为 f 在 x=a 处的微分, 它是当 x 从 a 变化为 a+△x 时 f 的变化量的近似. 这意味着 x 的微小变化会引起 y 的变化, 而后者的变化量约为前者的 f'(x) 倍.
18 牛顿法
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(y)=0的根。
牛顿法假设a 是对方程 f(x) = 0 的解的一个近似. 如果令 b = a - f(a)/f′(a). 则在很多情况下, b 是个比 a 更好的近似.
有时牛顿法也会不起作用.
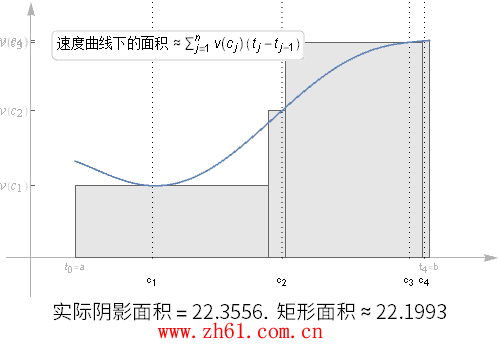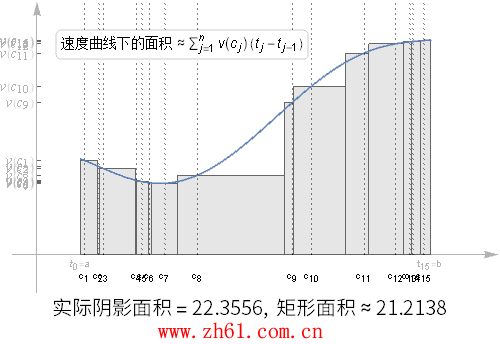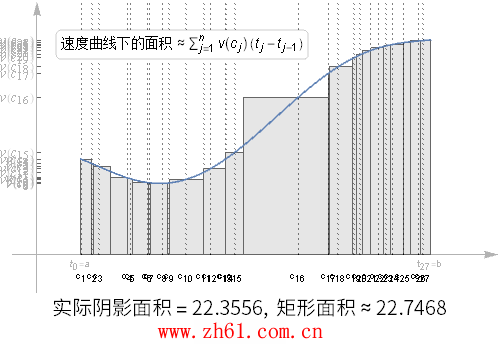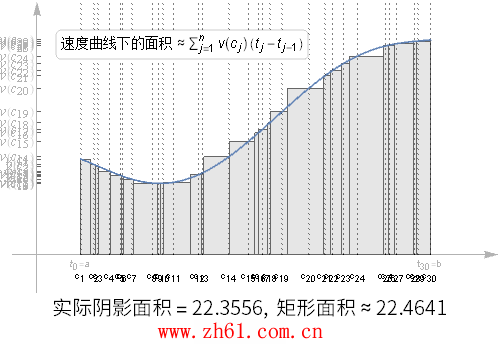
19 速度曲线下的面积
现在考虑速度为时间 t 的连续函数, 在整个[a, b] 区间内重复这个划分的过程, 在每个时间段内, 我们都取个样本速度.
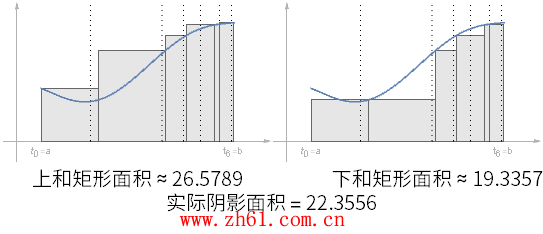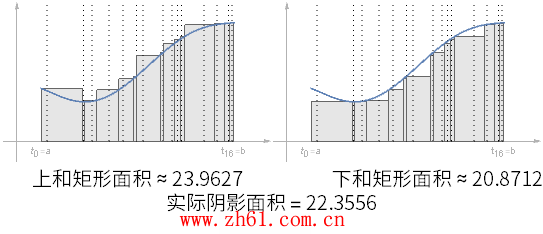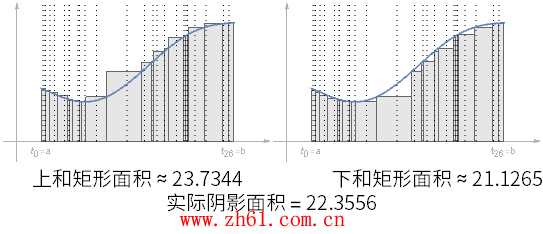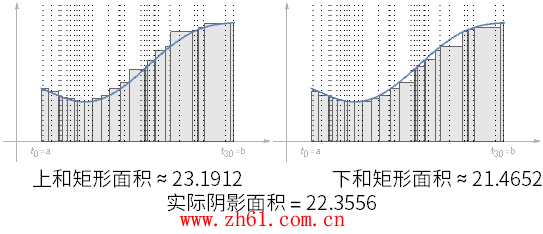
观察上动图随着划分区间增大, 阴影部分的面积比之前的分区更接近于真实面积了, 但是如果其中的某个分区很大, 对估算结果仍然会有很大的影响.
如果这些分区的最大值趋于 0 , 那么这个估算的结果就越来越精确了, 就得到了下面的公式:
因为最大区间趋于0, 这样划分的数目就会越来越大, 所以上述极限自动包含了n 趋于∞ 这样一个思想.
如果在不同的划分中选择函数的最大值和最小值, 所形成的矩形当然会不同
通过对这两种情况的分析, 可以得到下和<=><>.
20 定积分
定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。即由 y=0,x=a,x=b,y=f(X)所围成图形的面积。把函数在某个区间上的图象[a,b]分成n份,用平行于y轴的直线把其分割成无数个矩形,再求当n→+∞时所有这些矩形面积的和。
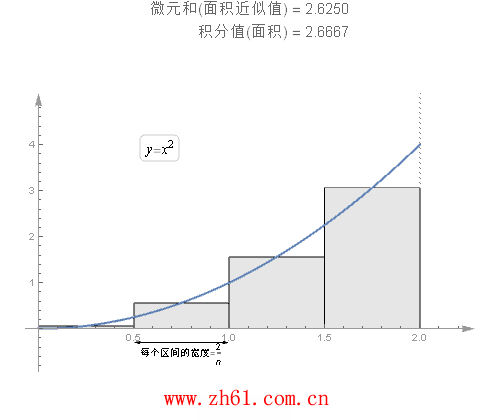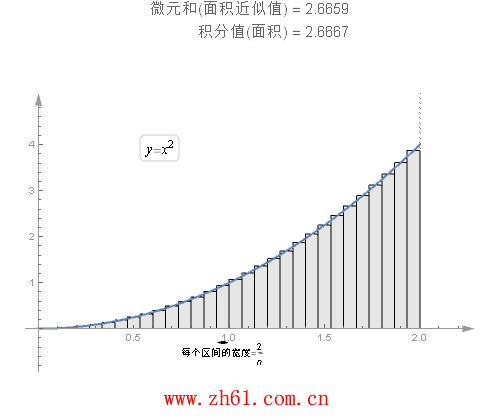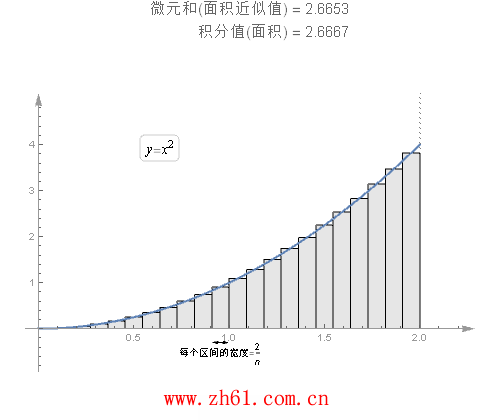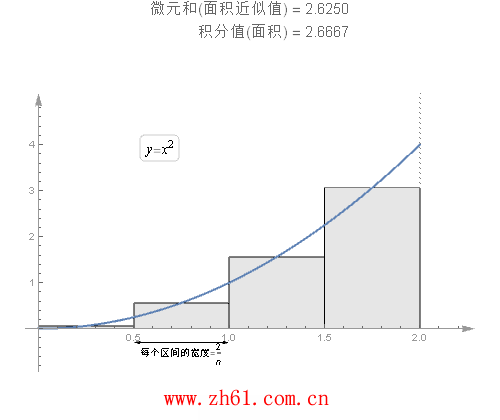
一个使用定义的例子:
需要把 [0,2] 区间分成n 个小区间, 每个小区间的长度是相等的. 因为总长度为2, 共有n 个区间, 所以每个区间的长度为2/n.
注:(1/3x^3)'=x^2
21 用其他函数的积分来表示的函数
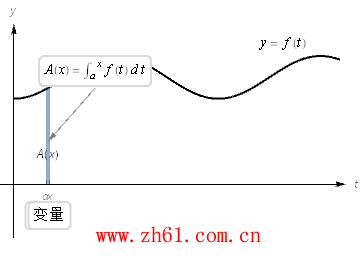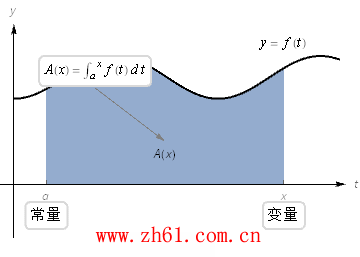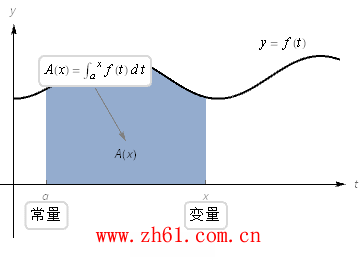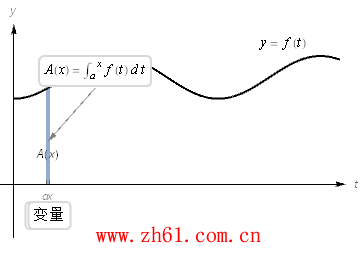
考虑积分下面积分式子实际上是一个以积分上线 x 为变量的函数, 这就有
观看下面的动画:
22 微积分的第一基本定理(The First Fundamental Theorem)
微积分的第一基本定理揭示了定积分与被积函数的原函数或者不定积分之间的联系。
如果函数f 在闭区间 [a,b] 上是连续的, 定义F 为
则 F 在开区间 (a,b) 内是可导函数, 而且 F'(x)=f(x)
观察下面的图形:
上图淡红色的阴影部分, 当 h 很小的时候几乎为小竖条, 所以可以用计算长方形面积的方法来估算该竖条的面积, 它的底从x 到x+h, 高从0 到f(x), 所以面积是 h*f(x) , 也就是:
Reference:《图解普林斯顿微积分读本》http://www.toutiao.com/a6480520623834530318/-End-

 更多
更多










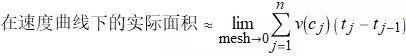
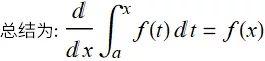


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底