逃逸速度是一个物体永久地逃离天体引力束缚的最小速度。

月球其实是有一个大气层的，它的学名为外逸层。它是如此的稀薄，以至于它的粒子很少碰撞。它稀薄的原因是月球的引力微弱不像地球那样，以至于它无法抓住在上方盘旋或从内部渗出的气体。

 
▲图片说明：月球陨石坑

月球有一个所谓的外逸层。

月球岩石释放的大部分气体粒子以大于月球逃逸速度的速度向上飞去，此速度便是一个物体永久逃逸一个天体的引力场，且永远不会回来的最小速度。

逃逸速度

现在，由于物体的重力场强度是其质量的函数，很明显，从大质量天体上逃逸更加困难。自然地，地球的逃逸速度比月球大得多，但比木星要小得多，因为木星的体积巨大，它在所有行星中拥有最高的逃逸速度。

 
▲图片说明：离开地球的最低速度为11.2 km/s（约为40,320 km/h或25,000 mph）。但是，在地球轨道上，离开太阳系的最低速度却是42.1 km/s 。

速度对于质量的依赖会造成一个矛盾的问题：我们在向比地球更大的行星发送探测器时，探测器必须携带大量剩余的燃料，因为它所需燃料量要比它燃烧的燃料量大得多，才能起飞和逃离地球。然而，当它在旅途中携带这些额外的燃料时，它会变得更重，因此更难加速到地球的逃逸速度。

 
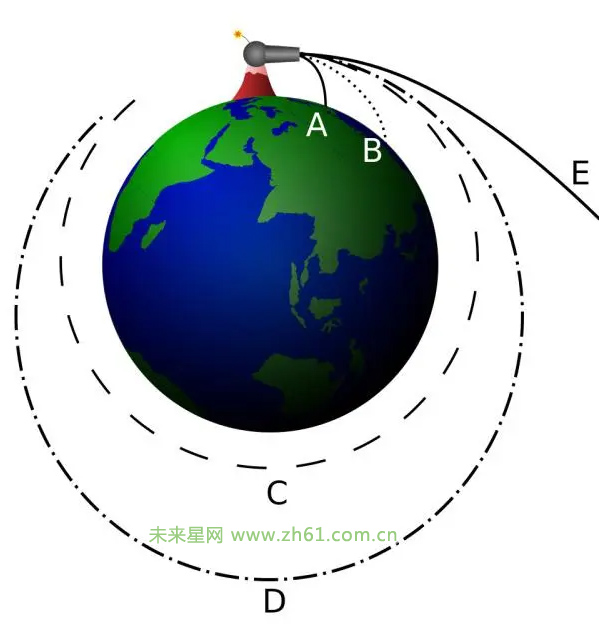
▲图片解释：A: 跌落地球<7.9 km/s B: 跌落地球 C: 圆周运动 = 7.9 km/s D: 椭圆轨道 E: 逃逸 > 11.2 km/s。

火箭的轨迹

 
▲火箭必须以11.2公里/秒的速度飞行，才能脱离地球引力束缚。

逃逸速度公式

只有当物体的动能等于它的重力势能时，才能逃离质量为m的天体。以V速度运动的质量为m的物体的动能为mv。根据定义，这个物体的重力势能是它离天体中心距离r的函数，公式为GMm/r，其中g是引力常数，其值为6.673*10^(-11)Nm^2kg^(-2)。由动能定理和万有引力公式，将两者构建等式，我们得出：

 
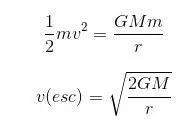
我们可以用这个方程中m和r的不同值来确定不同天体的逃逸速度。r的影响也意味着高出天体表面的物体比在r表面上的物体更容易逃脱。这是显而易见的，因为当我们离开行星表面时，它的引力强度会降低。

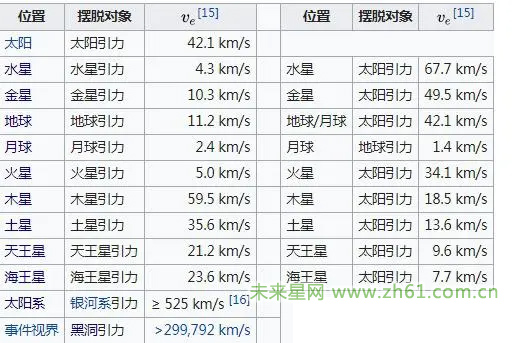
逃逸公示表

最后，我们可以从方程中推断出行星的逃逸速度与物体的质量无关。这是违反直觉的，但无论是恐龙还是乌龟，它必须以11.2公里/秒（忽略空气阻力）的速度逃离地球！然而，加速度是质量的函数，所以即使恐龙以与乌龟相同的速度逃逸，将其加速到11.2公里/秒仍比将乌龟加速到同速要困难得多。

 
相关知识

宇宙速度，是指物体从地球出发，要脱离天体重力场的四个较有代表性的初始速度的统称。

航天器按其任务的不同，需要达到这四个宇宙速度的其中一个。例如人类第一个发射成功的星际探测器月球1号就需要达到第二宇宙速度，才能摆脱地球重力。而旅行者2号则需要达到第三宇宙速度，才能离开太阳系。

 
▲图片说明：月球1号是首个达到第二宇宙速度的太空探测器。

宇宙速度的概念也可应用于在其他天体发射航天器的情况。例如计算火星的环绕速度和逃逸速度，只需要把公式中的M,R,g换成火星的质量、半径、表面重力加速度即可。