第16 章 定积分
16.1 基本思想
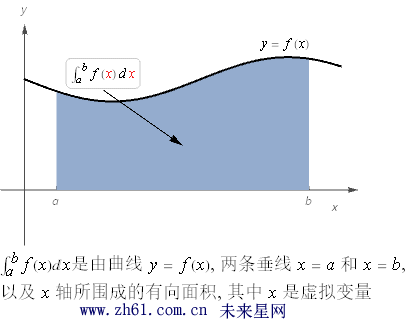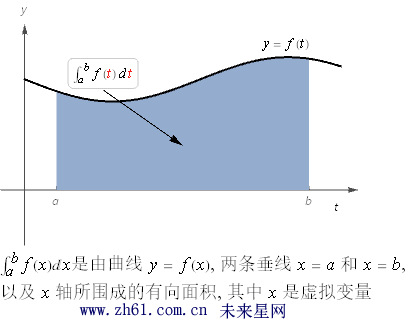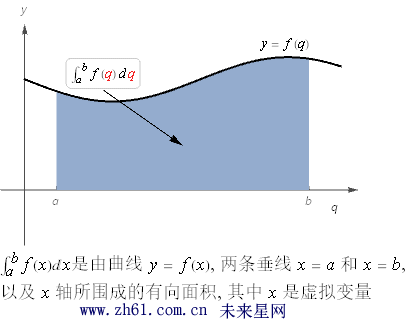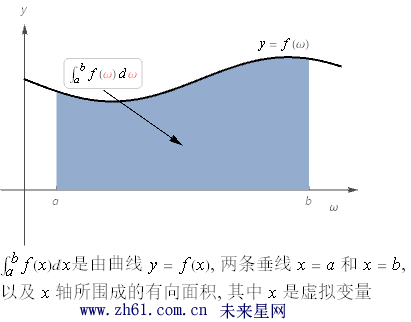
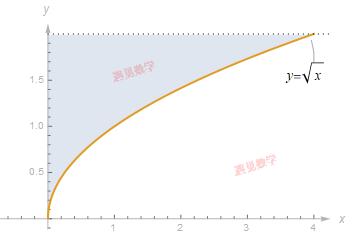
们从一个函数以及 [a,b] 区间开始研究. 画出 y = f(x) 这个函数图像, 考虑该曲线, x 轴和两条垂直线 x = a 和x = b 所围成的面积.
积分变量是虚拟变量可以用任意符号:
定积分就是函数 f(x) 对于x 从a 到b 的积分:
表达式 f(x) 是被积函数(Integrand), a 和b 说明两条垂线在哪, 也叫积分端点.
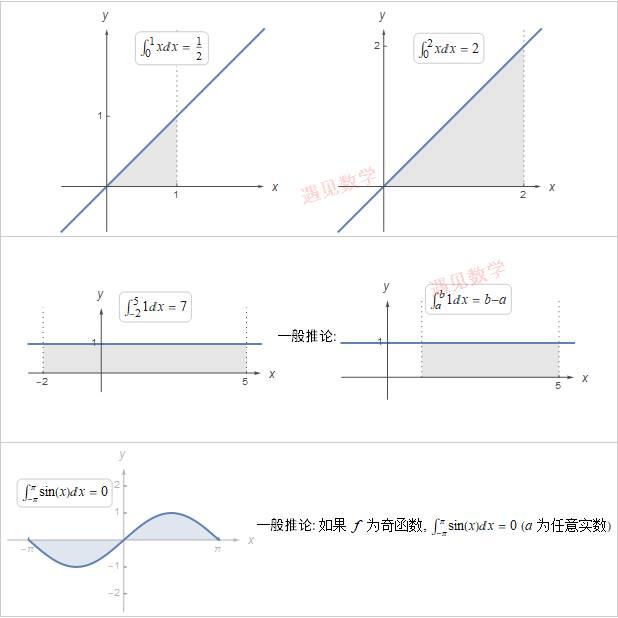
一些简单的例子
考虑下面几个定积分以及相应图形:
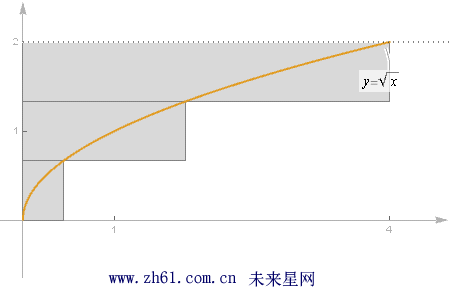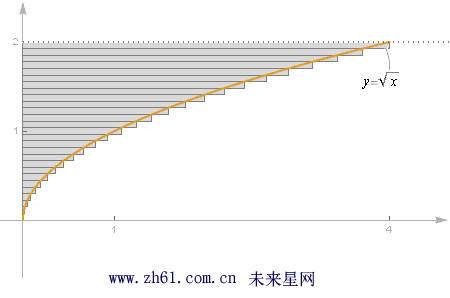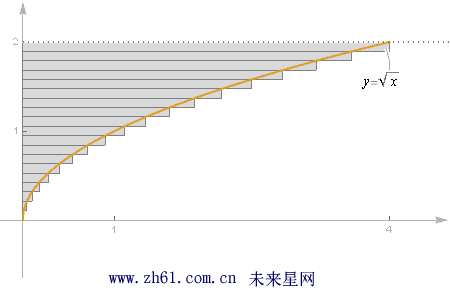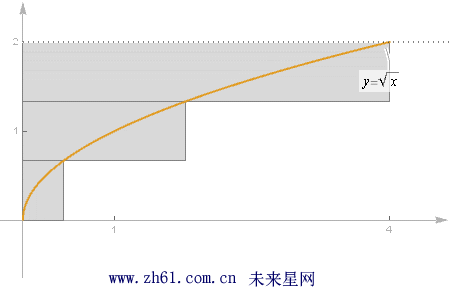
16.2 定积分的定义(Definition of the Definite Integral)
一个使用定义的例子
需要把 [0,2] 区间分成n 个小区间, 每个小区间的长度是相等的. 因为总长度为2, 共有n 个区间, 所以每个区间的长度为2/n.
16.3 定积分的性质(Properties of Definite Integrals)
16.4 求面积
16.4.1 求通常的面积
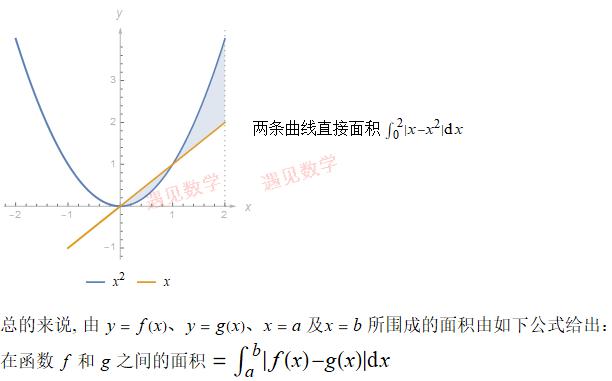
16.4.2 求解两条曲线之间的面积
16.4.3 求曲线与y 轴所围成的面积
要正确地计算面积, 最好的方法是对y 求积分, 而不对x 求积分. 我们可以把该面积按水平的方向切成条状, 而不是竖条.
如 果f 存在反函数, 就是由函数y = f(x)、直线y = A 和y = B 以及y 轴所围成的面积.
16.6 积分的平均值和中值定理
可以在区间 [a, b] 内, 将可积函数f 的平均值定义为:
积分的中值定理(Mean Value Theorem for integrals):函数 f 在区间 [a,b] 上连续, 那么在开区间 (a,b) 内总有一点 c, 满足:
简言之, 连续函数在一段区间内至少一次达到它的平均值.
16.7 不可积的函数(A Nonintegrable Function)
如果函数 f 为有界函数并在区间 [a, b] 上有有限个不连续点, 那么函数f 是可积的. 也就是说, 定积分存在.
现在看一个有太多个不连续点的函数的积分情况. 对于区间 [0, 1] 内的数 x:
函数 f(x) 的值在高度1 和2 之间来回跳跃, 实际上在任何一点都不连续, 所以 f 不可积的. 实际上有一种方法可以求这种函数的积分, 叫作勒贝格积分(Lebesgue integration).
(本章完)
「予人玫瑰, 手留余香」
转发即帮助[遇见数学]更快发展, 非常感谢!

 更多
更多

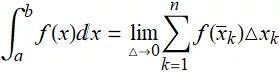
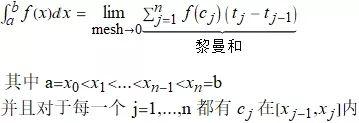



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底