第6 章求解微分问题
6.1 使用定义求导
上一节已经学习到了导数的定义, 可以使用它来求解给出函数的导数, 在从分子分母中消去 h, 然后通过设 h = 0 求极限值, 现在列出常见函数的导数结果:
6.2 用更好的办法求导
一旦掌握了如何用定义来求导的方法, 就可以根据一些简单的法则由已经求得的导数来构造其他的导数了, 书中有详细的推导过程, 这里不再赘述, 只讲结论摆出来, 下面常用的那些会用到的求导法则:
6.2.7 乘积法则和链式求导法则的理由
推荐查看《微积分的本质》相应第 4 部分内容: 《直观理解链式法则和乘积法则》里边用图形的方式解释的很清楚.
6.3 求切线方程
求导的一个好处就是可以使用导数来求所给曲线的切线方程. 求出过该点的切线的斜率是 f' (x), 使用点斜式来得到切线方程.
6.4 速度和加速度
求导的另一个应用是计算运动物体的速度和加速度. 一个物体沿着实轴运动. 我们发现, 如果在时刻t 它的位置是 x, 那么它在时刻 t 速度就是对 x 求一阶导.
速度是位置的瞬时变化比率, 物体的加速度是速度的瞬时变化比率. 也就是说, 加速度是速度关于时间t 的导数. 由于速度是位置的导数, 加速度实际上是位置 x 的二阶导.
6.6 分段函数的导数
6.7 直接画出导函数的图像
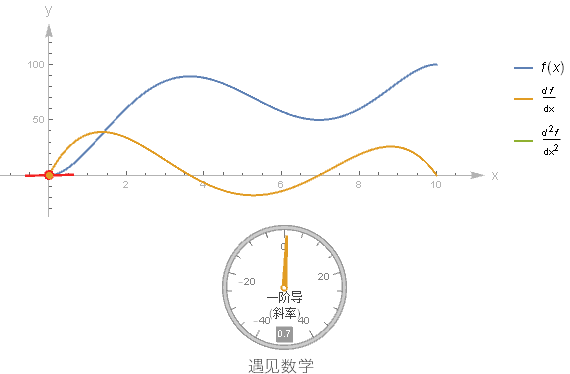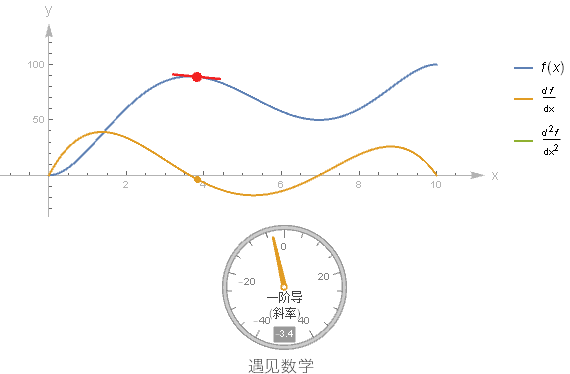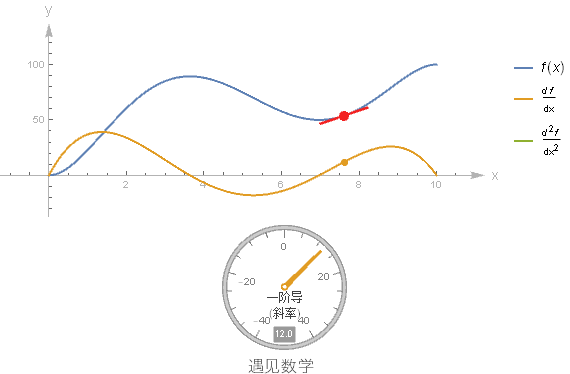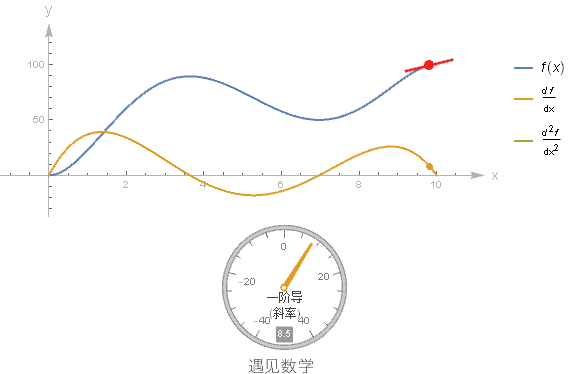
假设有一个函数的图像, 你不知道它的方程, 但又想要画出其导函数的图像, 这就需要你对微分有一个很好的理解. 这里制作一个动图来加深对导函数的印象, 推荐阅读书中对应的此节内容.
(本章完)

 更多
更多
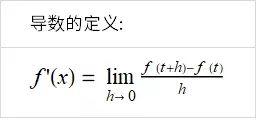


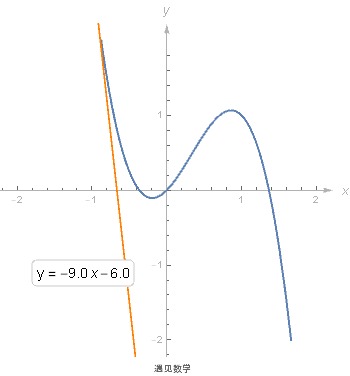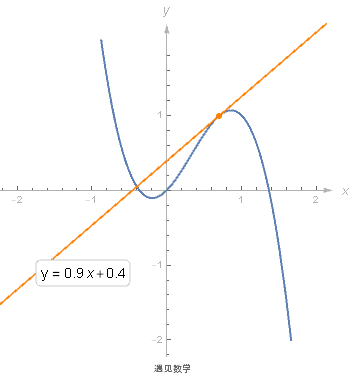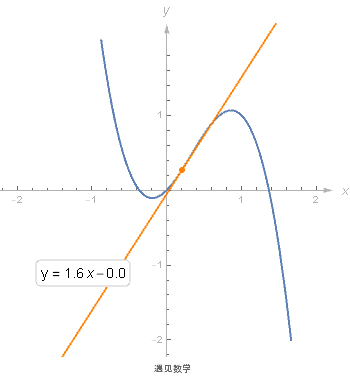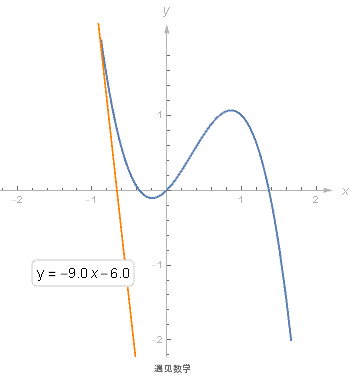
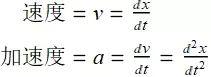

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底