力矩表示力对物体作用时所产生的转动效应的物理量。力和力臂的向量积为力矩。力矩是矢量（vector）。力对某一点的力矩的大小为该点到力的作用线所引垂线的长度（即力臂）乘以力的大小，其方向则垂直于垂线和力所构成的平面用力矩的右手螺旋法则来确定。力对某一轴线力矩的大小，等于力对轴上任一点的力矩在轴线上的投影。国际单位制中，力矩的单位是牛顿·米。常用的单位还有千克力·米等。力矩能使物体获得角加速度，并可使物体的动量矩发生改变，对同一物体来说力矩愈大，转动状态就愈容易改变。

中文名:力矩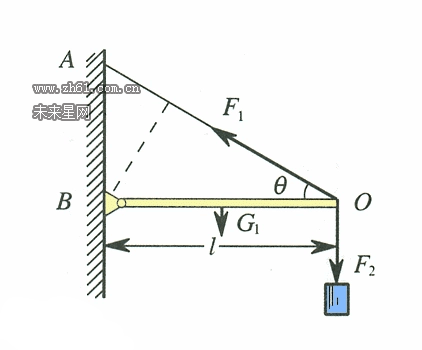
外文名:torque;moment of force
单  位:牛顿·米(N·m)
应用学科:物理
表达式:M=L×F矢量性矢量

定义
力矩 (moment of force) 力对物体产生转动作用的物理量。可以分为力对轴的矩和力对点的矩。即：M=L×F。其中L是从转动轴到着力点的距离矢量，F是矢量力；力矩也是矢量。
 
力对点的矩
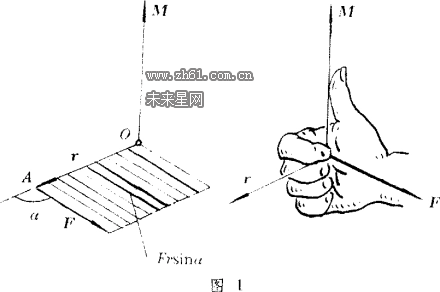
力矩是量度力对物体产生转动效应的物理量。可分为力对点的矩和力对轴的矩。力对某一点的矩是量度力对物体作用绕该点转动效应的物理量。力F对某点O的力矩定义为：力F的作用点A相对于O点的矢径r与力F的矢积用M0(F)表示，M0(F)=r×F，力对点的矩是矢量，大小等于F的大小与O点到F的作用线的垂直距离d（称为力臂）的乘积，或者等于以r、F为邻边的平行四边形的面积rFsinα，α是r与F夹角。M0(F)方向垂直于r与F所组成的平面，r、F、M。(F)三者满足右手螺旋关系。对空间任何点都可以定义力对点的矩。由于力对点的矩依赖于力的作用点的位置矢径r，所以同一个力对空间不同的点的力矩是不同的。当力的作用线过空间某点，则该力对此点的矩为零。如果有几个共点力（作用点为A）Fi(i=1，2，……，n)作用于物体，合力F=F1+F2+…+Fn，则合力对O点的力矩M0(F)=r×(F1+F2+……+F)=r×F1+r×F2+…+r×Fn=M01+M02…+M0n，即合力对某点O的力矩等于各分力对同一点力矩的矢量和。矢量M0(F)称为此力系对O点的主矩。

 
力对轴的矩
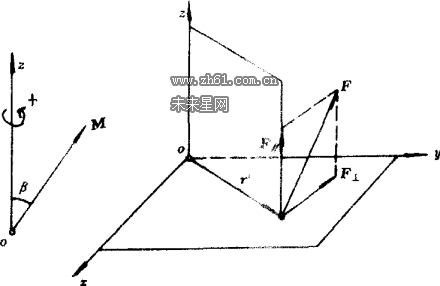
力对某轴的矩是量度力对物体作用绕该轴转动效应的物理量。定义为，力F对O点的力矩M在过O点的任一轴线OZ轴上的投影称为力F对OZ轴的力矩，用Mz表示，Mz=Mcosβ，β为矢量M与OZ轴正方向的夹角，并规定物体转动正方向与OZ轴正方向满足右手螺旋关系，如图2中箭头所示。Mz是一个代数量，其正负表示物体转动倾向，Mz>0表示力F使物体转动倾向与转动正方向一致，Mz<0则相反。必须指出，力F对OZ轴不同点的力矩是不同的，但这些力矩在OZ轴上的投影却是相等的。所以可以说力F对OZ轴上任一点力矩在OZ轴上的投影等于力F对OZ轴的矩。而如果力F平行于OZ轴或F的作用线与OZ轴相交则F对OZ轴的力矩为零。力F对OZ轴的矩还可定义为：力F在垂直于OZ轴的平面内的投影F⊥对该平面和OZ轴的交点O之矩在OZ轴上的投影：[Moz(F)]z=[M0(F⊥)]z=[r×F⊥]z。当Moz(F)方向与OZ轴正方向一致时为正，表示正对OZ轴箭头观察该力F有使物体逆时针转动倾向，否则便相反。或者Moz(F)的方向与物体转动倾向满足右手螺旋关系。对空间任意轴线都可以定义力对轴的矩。力矩的单位是牛顿·米(N·m)。