埃米·诺特（Emmy Noether）是一位杰出的德国数学家，她对现代数学的发展做出了重要贡献。她的研究领域涵盖了代数学、理论物理学、拓扑学等多个方向，她的成就不仅为学术界所赞誉，也为后来的数学家树立了榜样。

 

生平与早年

1882年，埃米·诺特出生在德国一个知识分子家庭。她从小就显示出对于数学的天赋，但由于当时女性在学术领域的局限，她在追求数学事业上遇到了困难。尽管如此，她仍然坚定地追求数学，并在1907年获得了哥廷根大学的博士学位。

 
埃米·诺特，是一位大器晚成的数学家，她在40岁左右才完成有决定性意义的工作，成为推动20世纪数学发展的杰出数学家。

诺特生活在公开歧视女性发挥数学才能的制度中，她的成就，既得益于家庭的熏陶，又受限于时代的局限。

爱因斯坦称赞她是“自女性开始受到高等教育以来最杰出和最富有创造性的数学天才”。

陈省身赞美她是“抽象代数领导人之一，大家公认为女性中最伟大的数学家，放在男性数学家中也绝对是第一流”。

1882年3月23日，埃米·诺特出生在德国埃朗根，一个富裕的犹太人家中。

祖父赫尔曼·诺特是经营木材加工的犹太富商，祖母是另一位犹太富商之女，对数学研究有浓厚的兴趣。

父亲马克斯·诺特是一位数学家。虽然儿时得了小儿麻痹症，但通过家庭教育和自学，他考入了海德堡大学。（海德堡大学成立于1386年，是德国最古老的大学，也是罗马帝国继布拉格大学和维也纳大学之后开设的第三所大学），他本来更喜欢天文学，但考虑做实践行动不便，就选了数学系。按照当时的风尚，在大学期间，每一位学生都需要在另一所大学学习一年。他选择了哥廷根大学（哥廷根大学是1734年，由英国国王兼汉诺威国王乔治二世创办，旨在弘扬欧洲启蒙时代学术自由的理念），高斯、狄利克雷和黎曼等数学大师都是哥廷根数学派的灵魂人物。1868年马克斯获得博士学位，成为诺特家族的第一位博士，此后在埃朗根大学教学，成为19世纪代数几何学的带头人之一。母亲也是一位犹太富商的女儿。

诺特虽然家境优越，但并不娇气，不化妆，也不注重打扮。

从父亲开始，诺特本人、诺特弟弟，诺特弟弟的儿子，都是数学家，诺特家族祖孙三代出了四位数学家，这在历史上是不多见的，更著名的数学家族是伯努利家族和中国的梅文鼎家族。

7岁，诺特进入小学读书，她在童年时代并没有显出过人的才能，只是班里一个普通的孩子。

12岁，诺特在埃朗根初级女子中学读书，她对那些专门为女孩子开设的宗教、钢琴、舞蹈等课程毫无兴趣，却非常喜欢外语学习，上法语和英语课时兴致很高。

1897年，15岁的诺特初中毕业，考入埃朗根私立高级女子学校。和其他女子高中一样，这所高中不重视数学。

1900年4月，诺特高中毕业了，她毫不费力地通过了英语和法语两门课的中学教师资格考试。

那时，读到高中，学历就算到头了。当时的德国，不提倡女孩子做科研，读书只是为了成为一个有文化教养的家庭主妇。

难道一辈子就做个中学老师？

她不甘心。

她只想坚持自己的理想，学数学！

受家庭的熏陶，诺特从小就在数学的环境中成长，父亲的学生和同事经常来家里讨论问题。父亲用一盘水果给姐弟俩讲集合论，把一盘苹果看成一个有限集合，每个苹果都是这个集合里的一个元素，几个苹果组成的集合，就是原来集合的子集。削马铃薯时，父亲的同事哥尔丹告诉她，任意小的邻域内，都既有属于马铃薯又有不属于马铃薯的点，所有这些点的集合成为马铃薯的边界。

大家相互尊重又无拘无束地各抒己见，热烈而又智慧的氛围，她和弟弟都喜欢上了数学。

于是她选了一条艰难的多的道路——进大学深造数学。

除了自身的努力，还有和时代的抗争。

法国，1861年允许女性读大学；

英国，1878年接受女性读大学；

意大利，1885年接受女性读大学。

而德国，直到1900年，还不允许女性注册大学，即便得到教师的允许，女性也只能旁听。

历史学家特雷斯克甚至认为：“近来有不少人谈论大学向女性开放的问题，这是很不体面的，也是不道德的，实际是向不合理的要求让步。大学是讲授科学和学问的机构，女性的智力不适宜在大学学习，而且她们在大学的存在将有碍青年完美品质的形成。”

尽管如此，诺特还是坚持向既定目标前进。

好在父亲是埃朗根大学的知名教授，1900年，诺特取得旁听生资格。在校的986名学生中，只有两名女旁听生。

埃米在大学选修数学和外语，她从学习解析几何和微积分开始。

三年的大学生活，诺特专注读书，潜心学问，独来独往。

1903年，诺特旁听了所有课程并顺利通过了结业考试。

也是这一年，法国的居里夫人获得诺贝尔物理学奖，是历史上第一个获得诺比尔奖的女性，这对诺特是极大的鼓励。

1903年秋，诺特效仿父亲，也去了哥廷根大学旁听，这是高斯和黎曼学习和工作过的地方。

20世纪初，哥廷根大学有“数学的麦加”的美誉，希尔伯特是当时数学界的领军人物，以一己之力，教出了76位博士高徒。他直率纯真，平易近人，很受年轻人的喜爱，而且讲课讲的很慢，经常重复，生怕有人听不懂。

诺特就在这样的环境中成长着。

1904年，她的家乡，埃朗根大学取消了不招女生的禁令，诺特立刻返回家乡，正式注册为大学生，入读研究生课程，是数学系47名学生中唯一的女生。

不久后，父亲的同事哥尔丹，同意做她的博士生导师。哥尔丹一生只培养了一名博士生，那就是诺特。

哥尔丹大半生研究不变量，被称为“不变量之父”，据说，他的一篇论文里，居然连着20页全是密密麻麻的公式，中间不见一个文字。

诺特也因此步入了不变量的王国，诺特的博士论文为《三元四次型不变量的完全系》。

1908年7月，诺特获得了埃朗根大学哲学博士学位，成为德国历史上第一位数学女博士。

但不公平的是，她在自己的祖国，连一份收入微薄的工作都得不到。

按照当时的规定，女性是不能当大学讲师的，更不要说教授了。

从1908年到1915年，她一直在埃朗根大学数学研究所工作，当然，没有工资。

1915年，爱因斯坦的广义相对论引起了数学界的轰动，1916年，诺特被希尔伯特邀请去了哥廷根大学。

在这里，诺特再一次感受到了时代的不公，那些男教授激烈反对诺特成为大学讲师，仅仅因为她是女性。

1918年，第一次世界大战以德国战败告终，这场战争给德国带来了历史上一定程度的进步，许多旧法令和旧制度发生变化，废除了限制和歧视女性的一些规定。

诺特再一次递交讲师资格申请书，终于获得了“非官方讲师”的头衔，她可以讲课了，但是，依然没有工资。

虽然没有工资，但毕竟有了正式的授课资格，诺特很知足。

1922年，40岁的诺特发表了《环中的理想论》，因为这篇论文的影响，诺特被誉为是“现代数学代数化的伟大先行者”，“抽象代数之母”。人们为她奔走呼告，诺特成了“非官方副教授”，但依然没有工资，人们帮她再三争取，才只有微薄的工资，仍低于一般的副教授。

诺特不追求金钱和荣誉，心中只有数学。

她培养了10多位博士，其中还有一位中国学生曾炯之，曾炯之在德国进修7年，获得哥廷根博士学位后回国，先后在浙江大学、北洋大学、国立西北联合大学、西北工学院及西康技艺专科学校担任教授。诺特十分看中曾炯之，在她因为犹太身份被迫离开德国之际，还叮嘱曾炯之一定要完成博士学位。

她一直在哥廷根大学教学，直到1933年被纳粹政府解雇。

大批知名的犹太籍科学家和学者被迫离开德国，前往美国。在1933-1934年间，德国的大学里就有大约7000人逃往美国。到1940年间，德国大约损失了500多名自然科学教授，450名医学教授和300名人文科学教授，导致德国学术倒退至几十年前的水平。

1933年8月，51岁的诺特乘船前往美国。

一边在布林莫尔女子文理学院Bryn Mawr College任教，一边在普林斯顿Princeton任教。

到美国一年多后，1935年4月14日，诺特因病在美国去世。

她曾经是充满生命活力的典范，

以她那刚毅的心情和生活的勇气，

坚定地屹立在我们这个星球上，

所以大家对此毫无思想准备。

她正处于她的数学创造能力的顶峰。

她那深远的想像力，

同她那长期经验积累起来的技能，

已经达到完美的平衡。

她热烈地开始了新问题的研究。

而这一切现在突然宣告结束，

她的工作猝然中断。

坠落到了黑暗的坟墓，

美丽的、仁慈的、善良的，

他们都轻轻地去了；

聪颖的、机智的、勇敢的，

他们都平静地去了；

我知道，但我决不认可，

而且我也不会顺从。

 

重要成就

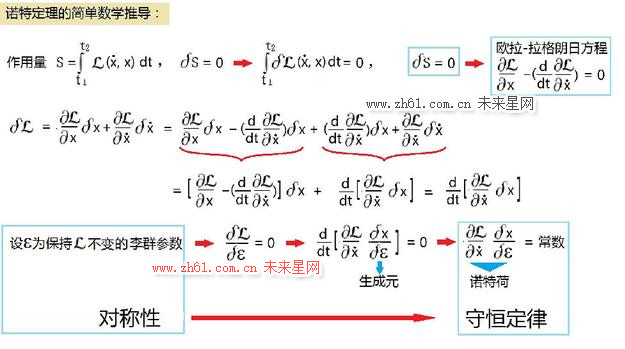
1. 诺特定理：诺特最为人称道的成就之一便是诺特定理，这一定理为理论物理学和代数学的发展带来了革命性的影响。该定理揭示了对称性与守恒量之间的关系，即每个对称性都对应着一个守恒量。通过诺特定理，我们可以更好地理解能量、动量、角动量等物理量的守恒，并为它们的应用提供了数学的基础。

 
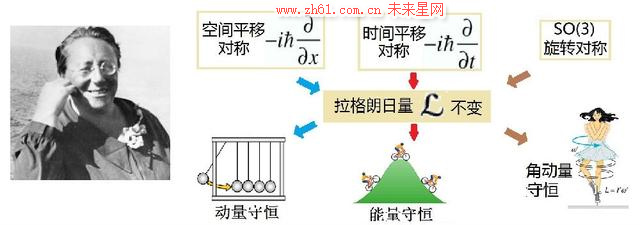
考虑一个物理系统，其中包含几个物理量，如能量、动量、角动量等。根据诺特定理，如果这个系统在某个方面具有对称性，比如平移对称性，那么就会存在一个与之对应的守恒量，这里是动量。换言之，物理系统中的动量守恒可以从空间平移对称性推导出来。这个定理在理论物理学中起到了至关重要的作用，帮助物理学家理解和预测各种自然现象。

 
2. 环和模论：埃米·诺特在环和模论方面作出了重要贡献。她的代数研究帮助我们理解抽象代数中的环、模、同态等概念，并深化了对于这些数学结构的认识。她的工作为现代代数学的发展奠定了基础。

 
举个例子，考虑整数集合Z。在整数集合中，我们可以定义加法和乘法运算，这使得Z成为一个环。在这个例子中，埃米·诺特的贡献之一是开发了Z的理论，研究了它的性质和结构。她的工作帮助我们更好地理解和应用整数集合中的代数运算。

 
3. 不变量理论：不变量理论是诺特在代数几何和群论领域的研究重点之一。她系统地研究了在变换下保持不变的量，并发展了一套数学工具来描述和分析这些不变量。这些工具在几何学和拓扑学中得到了广泛应用，并为后续研究提供了重要的基础。

举个例子，考虑一个平面上的图形，比如一个长方形。通过旋转、平移或镜像等操作，我们可以改变这个图形的位置和形状，但是某些性质可能保持不变。例如，长方形的面积在这些变换下保持不变。在这个例子中，埃米·诺特的工作为我们提供了一种方法来定义和计算这样的不变量，并研究它们的性质。

 
4. 拓扑学：在拓扑学领域，诺特的研究主要集中在代数拓扑方面。她对拓扑不变量进行了深入研究，如同调和同伦群等。这些不变量揭示了拓扑空间的重要性质，并对后来的拓扑学家产生了深远的影响。

例如，考虑一个环面，即类似于圆环形状的二维曲面。通过拉伸、挤压或弯曲等操作，我们可以改变这个曲面的形状，但某些基本的几何属性可能保持不变。埃米·诺特的工作为我们提供了一种方法来定义和计算这样的拓扑不变量，并研究它们的性质，从而帮助我们理解和分类不同类型的拓扑空间。

 

影响

埃米·诺特的工作对数学和理论物理学领域产生了深远的影响。她的成就被广泛认可，许多重要的数学和物理学奖项以她的名字命名，如诺特奖等。她的研究为现代数学打开了新的大门，激励了无数后来的数学家和科学家。

结语

埃米·诺特以其卓越的才华和对于数学的热爱成为数学界的先驱和奠基者。她的贡献在代数学、理论物理学和拓扑学等领域具有不可磨灭的意义。诺特的故事为我们展示了一个勇敢追求卓越的女性科学家的典范，激励着我们不断前行，探索未知的数学世界。让我们铭记并传承她的精神，为推动数学的发展做出自己的贡献。