偏心率（Eccentricity）是用来描述圆锥曲线轨道形状的数学量，定义为曲线到定点（焦点）的距离与到定直线（准线）的距离之比。对于椭圆，偏心率即为两焦点间的距离（焦距，2c）和长轴长度（2a）的比值，即e=c/a（偏心率一般用e表示）。

中文名:离心率
外文名:Eccentricity
又  称:偏心率
当e=0时:圆
当0<e<1时:椭圆
当e=1时:抛物线
当e>1时:双曲线
通用表示字母:e

概念
偏心率(离心率)
偏心率（Eccentricity）是用来描述圆锥曲线轨道形状的数学量。对于圆锥曲线（二次曲线）的（不完整）统一定义：到定点（焦点）的距离与到定直线（准线）的距离的商是常数e（离心率）的点的轨迹。
当e>1时，为双曲线的一支；当e=1时，为抛物线；当0<e<1时，为椭圆；当e=0时，为一点（详见百度百科圆锥曲线词条）。
对于椭圆，偏心率即为两焦点间的距离（焦距，2c）和长轴长度（2a）的比值，即e=c/a。偏心率反映的是某一椭圆轨道与理想圆环的偏离程度，长椭圆轨道“偏心率”高，而近于圆形的轨道“偏心率”低。
在椭圆的标准方程 (x/a)^2+(y/b)^2=1 中，如果a>b>0焦点在X轴上，这时，a代表长轴、b代表短轴、 c代表两焦点距离的一半，有关系式 c^2=a^2-b^2，即e^2=1-(b/a)^2。因此椭圆偏心率0<e<1，短轴与长轴比值(b/a)越小，e越接近于1，椭圆也就越扁平。

 
行星的偏心率
德国天文学家开普勒（1571--1630），他从第谷·布拉赫对行星运动的观察结果中推导出太阳系中行星运动的三大定律：

行星轨道偏心率
1.每个行星在椭圆轨道上环绕太阳运动，而太阳在一个焦点上。
2.太阳和行星的矢径在相等的时间间隔中扫过相等的面积。
3.行星的轨道周期的平方与它的轨道的长轴的三次方成正比。
开普勒定律是纯几何学的描述，它们描述了一个单一质点绕一个固定中心的运动。它在理论上可以借由牛顿第二定律以及牛顿万有引力定律来证明。尽管开普勒定律阐明的是行星绕太阳的轨道运动，但它们可以适用于任意二体系统的运动，如相互绕转的双恒星系统、地球和月亮、地球和人造卫星等。开普勒定律在大量的天文观测事实中得到了验证。
点卫星在点中心体场中的轨线称为开普勒轨道，开普勒轨道是圆锥曲线，点中心体位于一焦点。
椭球的偏心率（Eccentricity of Elliopsoid）

 
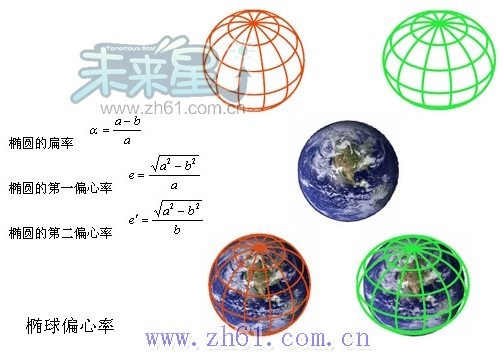
同样可以定义椭球的偏心率（Eccentricity of Elliopsoid）来描述椭球体相对于球体的扁平程度。例如，地球并不是一个理想球体，而是近似椭球（地球赤道半径6378.137千米，极半径6356.752千米）。地球扁率（椭球扁率是椭球偏心率定义之一）是描述地球形状的主要参数之一，其计算以赤道半径（长半轴a）和极半径（短半轴b）的差除以赤道半径，即(a-b)/a=0.00332。