微分几何学知识
径矢(矢径)
在直角坐标系中由原点o到任意点P的点矢![]() =o
=o![]() ,称为点P在坐标系中的径矢。
,称为点P在坐标系中的径矢。
设径矢![]() 在坐标轴上的投影分别为:ax
在坐标轴上的投影分别为:ax![]() 、ay
、ay![]() 、az
、az![]() ,则径矢坐标式为
,则径矢坐标式为![]() =ax
=ax![]() +ay
+ay![]() +az
+az![]() ,其模为
,其模为![]() 。若径矢与坐标轴之间的夹角分别为α、β、γ则a=cos-1(ax/|
。若径矢与坐标轴之间的夹角分别为α、β、γ则a=cos-1(ax/|![]() |);β=cos-1(ay/|
|);β=cos-1(ay/|![]() |) ;γ=cos-1(az/|
|) ;γ=cos-1(az/|![]() |)。单位径矢在坐标轴上的分量分别为cos α、cos β、cos γ (见图4-4)。
|)。单位径矢在坐标轴上的分量分别为cos α、cos β、cos γ (见图4-4)。
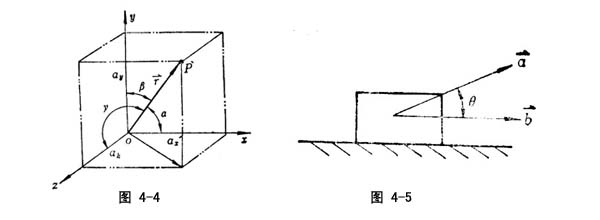
矢量的数积(标积、内积、点积)
矢量![]() 和矢量
和矢量![]() 的数积是纯量,定义为:
的数积是纯量,定义为:![]() ·
·![]() =|
=|![]() ||
||![]() |cosθ=abcosθ,θ为矢量
|cosθ=abcosθ,θ为矢量![]() 、
、![]() 之夹角(图4-5)。设两矢量的分量分别为ax、ay、az ;bx、by、bz ,则两矢量的夹角为
之夹角(图4-5)。设两矢量的分量分别为ax、ay、az ;bx、by、bz ,则两矢量的夹角为![]() ,由定义可知
,由定义可知 ![]() 2=
2=![]() 2=
2=![]() 2=1,
2=1, ![]() ·
·![]() =
=![]() ·
·![]() =
=![]() ·
·![]() =0,两矢量相互垂直的充要条件是它们的数积为零。
=0,两矢量相互垂直的充要条件是它们的数积为零。
矢量的矢积(外积、X积)
矢量![]() 和矢量
和矢量![]() 的矢积为矢量,定义为:
的矢积为矢量,定义为:![]() ×
×![]() =|
=|![]() ||
||![]() |sinθ
|sinθ![]() ,θ为
,θ为![]() 、
、![]() 之夹角,
之夹角,![]() 为垂直
为垂直![]() 、
、![]() 所在平面Σ的单位矢量(图4-6)。
所在平面Σ的单位矢量(图4-6)。![]() ×
×![]() =-
=-![]() ×
×![]() ,其坐标式为
,其坐标式为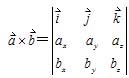
由定义知 ![]() ×
×![]() =
=![]() ×
×![]() =
=![]() ×
×![]() =0,
=0,![]() ×
×![]() =
=![]() ,
,![]() ×
×![]() =
=![]() ,
,![]() ×
×![]() =
=![]() 两矢量平行的充要条件是它们的矢量积为零。
两矢量平行的充要条件是它们的矢量积为零。
矢量混合积
矢量![]() 和矢量
和矢量![]() 求矢积后再和第三个矢量
求矢积后再和第三个矢量![]() 求数积称混合积,混合积是纯量,若已知矢量的坐标分量,则
求数积称混合积,混合积是纯量,若已知矢量的坐标分量,则![]() 、
、![]() 、
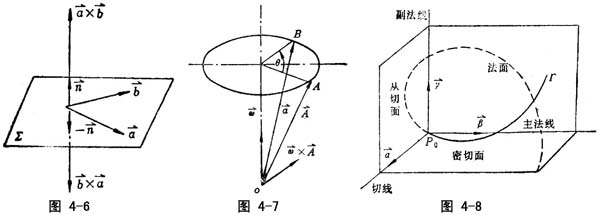
、![]() 的混合积为:
的混合积为: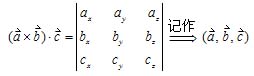
由定义知(![]() 、
、![]() 、
、![]() )=(
)=(![]() ,
,![]() ,
,![]() )=(
)=(![]() ,
,![]() ,
,![]() )=-(
)=-(![]() ,
,![]() ,
,![]() )=-(
)=-(![]() ,
,![]() ,
,![]() )=-(
)=-(![]() ,
,![]() ,
,![]() )。底矢的混合积恒等于1;三个矢量
)。底矢的混合积恒等于1;三个矢量![]() 、
、![]() 、
、![]() 共面的充要条件是它们的混合积等于零。
共面的充要条件是它们的混合积等于零。
三重失积
矢量![]() 、
、![]() 、
、![]() 的三重矢积定义为(
的三重矢积定义为(![]() ×
×![]() )×
)×![]() =(
=(![]() ·
·![]() )·
)·![]() -(
-(![]() ·
·![]() )·
)·![]() 。三重失积是矢量。
。三重失积是矢量。
矢量回转定义式
矢量![]() 绕回转轴
绕回转轴 ![]() 转过向角θ(图4-7),得新矢量
转过向角θ(图4-7),得新矢量![]() ,新旧矢量之间的关系式,
,新旧矢量之间的关系式,![]() =(θ
=(θ![]() )
)![]()
![]() 称矢量回转定义式。式中θ为有向角,逆时针为正;
称矢量回转定义式。式中θ为有向角,逆时针为正;![]() 表示回转符号。定义式的展开式为:
表示回转符号。定义式的展开式为:![]() =cosθ
=cosθ![]() (1-cosθ)·(ω·
(1-cosθ)·(ω·![]() )·
)· ![]() +sinθ·(
+sinθ·(![]() ×
×![]() )。
)。
拉格朗日恒等式
四个矢量![]() 、
、![]() 、
、![]() 、
、![]() 之间的关系式:(
之间的关系式:(![]() ×
×![]() )·(
)·(![]() ×
×![]() )=(
)=(![]() ·
·![]() )(
)(![]() ·
·![]() )-(
)-(![]() ·
·![]() )(
)(![]() ·
·![]() )称拉格朗日恒等式。
)称拉格朗日恒等式。
基本矢
设曲线Γ在P0点处的切矢为![]() ,这时
,这时![]() ⊥
⊥![]() (“·”表示对弧长求导),若在P0处k≠0,则
(“·”表示对弧长求导),若在P0处k≠0,则![]() 沿一条法线方向,这条法线称曲线Γ在P0点处的主法矢
沿一条法线方向,这条法线称曲线Γ在P0点处的主法矢![]() ,在曲线Γ上k≠0的非逗留点P0处,令
,在曲线Γ上k≠0的非逗留点P0处,令 ![]() =
=![]() ×
×![]() ,称
,称![]() 为P0点处的副法矢,于是符合右手定则又互相垂直的三个单位矢量
为P0点处的副法矢,于是符合右手定则又互相垂直的三个单位矢量![]() 、
、![]() 、
、![]() 称曲线Γ在P0点处的基本矢。三个基本矢分别组成了法面、密切面、从切面,如图(4-8)所示。
称曲线Γ在P0点处的基本矢。三个基本矢分别组成了法面、密切面、从切面,如图(4-8)所示。
曲线的基本公式
令![]() 、
、![]() 、
、![]() 为曲线在P点处的基本矢,于是在P点处可写出如下关系式:
为曲线在P点处的基本矢,于是在P点处可写出如下关系式: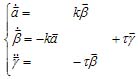
这些关系式称曲线的基本公式,式中k为曲率,τ为挠率。
曲线的切矢
若已知曲线Γ:![]() =
=![]() (t)t1≤t≤t2为连续曲线,则曲线P0点处的切矢定义为:如
(t)t1≤t≤t2为连续曲线,则曲线P0点处的切矢定义为:如![]() ′(t)≠0,保证曲线Γ在P0点处切线存在,而
′(t)≠0,保证曲线Γ在P0点处切线存在,而![]() ′(t0)代表这条切线方向,则称
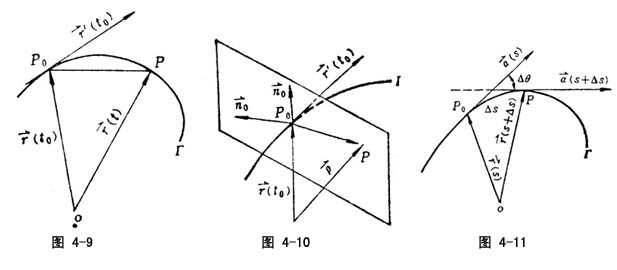
′(t0)代表这条切线方向,则称![]() ′(t0)为曲线Γ在P0点处的切矢(图4-9)。
′(t0)为曲线Γ在P0点处的切矢(图4-9)。
法线的规范方程式
设X、Y、Z为法线上任意点的坐标值,x、y、z为法线上给定点坐标值,法线方程为: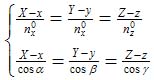 曲面Σ:当F=F(x,y,z)时
曲面Σ:当F=F(x,y,z)时 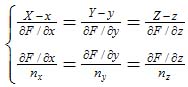
曲线的法面
若曲线Γ:![]() =
=![]() (t) ,在P0点的切线为
(t) ,在P0点的切线为![]() ′(t0),则垂直于切线的每一条直线都称为法线,法线所在的平面称曲线在P0点处的法面(图4-10)。
′(t0),则垂直于切线的每一条直线都称为法线,法线所在的平面称曲线在P0点处的法面(图4-10)。
设法面上的流动矢量为![]() ,则法面的矢方程为:
,则法面的矢方程为:![]() ′(t0)·[
′(t0)·[![]() -
-![]() (t0)]=0
(t0)]=0
曲率
曲线上任意点P处的曲率,表示了曲线在P点处邻近的弯曲程度,它是一个几何量。设P0为曲线上的固定点,P为P0的邻近点,对应弧长分别为s0和s0+Δs,P0和P点处两切线间的夹角为Δθ(图4-11),则定义![]() 为曲线在P0点处的曲率。若曲线Γ用
为曲线在P0点处的曲率。若曲线Γ用![]() =r(s)表示,则k=
=r(s)表示,则k=![]() =|
=|![]() |,若曲线Γ用
|,若曲线Γ用![]() =
=![]() (t) 表示,则k=|
(t) 表示,则k=|![]() ′×
′×![]() ″|/|
″|/|![]() ′|3。
′|3。
曲率线
曲面Σ上,若一条线的切矢总沿着主方向,则该曲线称曲面Σ上的一条曲率线。在不含有脐点的曲面上,参数曲线u、v为曲率线的充要条件是F=M=0。
短程曲率
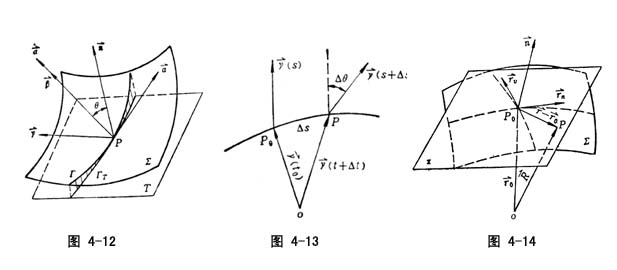
如图4-12所示,在曲面Σ上,取一条过P点的曲线Γ,并作过P点切面T, ![]() 为Γ在P点的切矢,
为Γ在P点的切矢, ![]() 为P点处曲面Σ的法矢,令
为P点处曲面Σ的法矢,令![]() =
= ![]() ×
×![]() (见图4-12),则曲线Γ上P点处的曲率矢量
(见图4-12),则曲线Γ上P点处的曲率矢量![]() 在
在![]() 上的投影,称曲线Γ在P点处的短程曲率kgo kg的表达式为:kg=
上的投影,称曲线Γ在P点处的短程曲率kgo kg的表达式为:kg= ![]() ·
·![]() =k
=k![]() ·
·![]() ,|kg|=ksinθ,k2=kn2+kg2。
,|kg|=ksinθ,k2=kn2+kg2。
法曲率
设在曲面Σ上的P点处,任意![]() 方向的法截线为
方向的法截线为![]() ,这条法截线在P点处的曲率称为曲面Σ在P点处沿
,这条法截线在P点处的曲率称为曲面Σ在P点处沿![]() 方向的法曲率。
方向的法曲率。
设曲面Σ:当![]() =
=![]() (u,v) ,则法曲率
(u,v) ,则法曲率![]() 或 kn=d
或 kn=d![]() d
d![]() /ds2=-d
/ds2=-d![]() ·d
·d![]() /d
/d![]() 2
2
挠率
若P0是曲线Γ上的任意点,P是Γ上P0点的邻近点,Δθ(Δθ>0)为Γ线上P0点与P点处副法线之夹角,弧长 ![]() =|Δs|,定义曲线Γ在P0点处的挠率为
=|Δs|,定义曲线Γ在P0点处的挠率为![]() (图4-13)。由此可见一条曲线为平面曲线的充要条件是|τ|=0 ,挠率的计算式为τ=(
(图4-13)。由此可见一条曲线为平面曲线的充要条件是|τ|=0 ,挠率的计算式为τ=(![]() ,
,![]() ,
,![]() )或
)或 ![]() 。
。
短程挠率
在曲面Σ上,在一条异于直线的短程线的P点处,该线切线方向的挠率,称短程挠率。![]() 。短程挠率等于零是主方向的充要条件。亦即曲面上一条曲线为曲率线的充要条件是沿其方向的短程挠率恒等于零。
。短程挠率等于零是主方向的充要条件。亦即曲面上一条曲线为曲率线的充要条件是沿其方向的短程挠率恒等于零。
界法矢
设P(2)是齿面Σ(2)上的二界共轭点,但不是一类界限点,在P(2)点处齿面Σ(1)的单位法矢![]() 0称为齿面Σ(2)在P(2)点处的界法矢。
0称为齿面Σ(2)在P(2)点处的界法矢。
渐近方向
在曲面Σ上的P点处,一般沿不同方向![]() 有不同的法曲率。特殊的kn=0的方向称为曲面Σ在P点处的渐近方向。
有不同的法曲率。特殊的kn=0的方向称为曲面Σ在P点处的渐近方向。
曲面的直角坐标式
若曲面的参数矢量式为Σ:![]() =
=![]() (u,v) ,则坐标式可写成:
(u,v) ,则坐标式可写成:
上式称曲面的直角坐标式(即坐标式)。
曲面的切矢
在曲面Σ的切平面π上,经过切点P0的每一条直线都和曲面Σ上的一些曲线相切,它们都称Σ曲面在ρ0的一条切线,而沿这些切线方向的矢量都叫做Σ曲面的切矢。
曲面的切面方程式
曲面P0点处,切线所在平面称切平面(图4-14)。设曲面Σ:![]() =
=![]() (u,v) ,
(u,v) ,![]() 为切面上任意点P的径矢,
为切面上任意点P的径矢,![]() 0为P0点的径矢,则(
0为P0点的径矢,则(![]() -
-![]() ,
,![]() u,
u,![]() v)=0称切平面方程式,亦即:
v)=0称切平面方程式,亦即: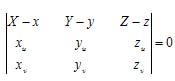
曲面的法线
与曲面Σ上P点处的切面相垂直,且通过P点的直线称曲面在P点处的法线。若曲面Σ:![]() =
=![]() (u,v) ,则法线矢量式为:
(u,v) ,则法线矢量式为: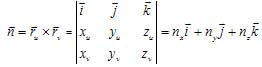 单位法矢量
单位法矢量 ![]() 。
。
 曲面的参数矢量式
曲面的参数矢量式
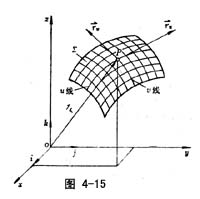
设u、v为曲面上的曲纹参数,并将u、v限制在区域G内(图4-15),记作(u,v)∈G,这时曲面的表达式为Σ:![]() =
=![]() (u,v),称其为曲面的参数矢量式。
(u,v),称其为曲面的参数矢量式。
寻常点(正则点)
设曲面Σ:![]() =
=![]() (u,v),则
(u,v),则![]() u×
u×![]() v≠0的点称曲面的寻常点,亦称曲面上的正则点。在该点有确定的法矢。
v≠0的点称曲面的寻常点,亦称曲面上的正则点。在该点有确定的法矢。
奇异点
设曲面Σ:![]() =
=![]() (u,v),则曲面上
(u,v),则曲面上![]() u×
u×![]() v=0的点称奇异点。
v=0的点称奇异点。
曲面的第一基本量
设曲面Σ:![]() =
=![]() (u,v),其上取曲线Γ:u=u(t),v=v(t),若Γ上没有奇点,选定参数t使u′(t),v ′(t)不同时为零,于是:d
(u,v),其上取曲线Γ:u=u(t),v=v(t),若Γ上没有奇点,选定参数t使u′(t),v ′(t)不同时为零,于是:d![]() u=
u=![]() udu+
udu+![]() vdv,则ds2=d
vdv,则ds2=d![]() 2=Edu2+Fdudv+Gdv2,称第一基本齐式,式中E=
2=Edu2+Fdudv+Gdv2,称第一基本齐式,式中E=![]() u2 ,F=
u2 ,F=![]() u
u![]() v ,G=
v ,G=![]() v2 ,三个纯量称第一基本量。第一齐式的判别式为:EG-F2=
v2 ,三个纯量称第一基本量。第一齐式的判别式为:EG-F2=![]() u2
u2![]() v2-(
v2-(![]() u·
u·![]() v )2,于是D= 或 。
v )2,于是D= 或 。
曲面的第二基本量
设曲面Σ上的任意曲线Γ:u=u(t),v=v(t),则称-d![]() ·d
·d![]() =Ldu2+2Mdudv+Ndv2的右侧为曲面的第二基本齐式。称L=-
=Ldu2+2Mdudv+Ndv2的右侧为曲面的第二基本齐式。称L=-![]() u·
u·![]() u,M=-
u,M=-![]() u·
u·![]() v,N=-
v,N=-![]() v·
v·![]() v为第二基本量。
v为第二基本量。
主曲率
在曲面Σ上的非脐点P处,沿不同的![]() 方向的法曲率是不相等的,称其中具有最大值和最小值的法曲率为曲面Σ在P点处的主曲率。
方向的法曲率是不相等的,称其中具有最大值和最小值的法曲率为曲面Σ在P点处的主曲率。
设曲面Σ:![]() =
=![]() (u,v)则主曲率可由公式:(EG-F2)kn2-(EN-2FM+GL)kn+(LN-M2)=0 求解。
(u,v)则主曲率可由公式:(EG-F2)kn2-(EN-2FM+GL)kn+(LN-M2)=0 求解。
主方向
在曲面Σ上的非脐点处,主曲率所在的切矢方向称主方向。主方向![]() 1和
1和![]() 2总是相互垂直的。对于脐点一切方向都是主方向。参数曲线u、v方向为主方向的充要条件是F=M=0,设曲面Σ:
2总是相互垂直的。对于脐点一切方向都是主方向。参数曲线u、v方向为主方向的充要条件是F=M=0,设曲面Σ:![]() =
=![]() (u,v),则Σ上任意点处的主方向可由下式确定:
(u,v),则Σ上任意点处的主方向可由下式确定: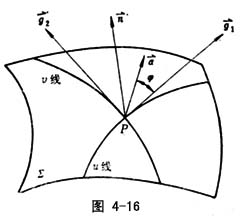
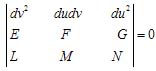
若k1、k2分别表示Σ上P点处主方向du=0,dv=0的主曲率,于是单位切矢![]() 1、
1、![]() 2:
2:
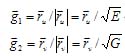
![]() 1、
1、![]() 2、
2、![]() 组成正交的右手系
组成正交的右手系![]() 1×
1×![]() 2=
2=![]() (图4-16)。
(图4-16)。
中曲率
曲面Σ:![]() =
=![]() (u,v)上任意点P处,若主曲率为k1、k2,则定义
(u,v)上任意点P处,若主曲率为k1、k2,则定义 ![]() 为中曲率。
为中曲率。
全曲率
曲面Σ:![]() =
=![]() (u,v)上任意点P处的主曲率为k1、k2,则定义
(u,v)上任意点P处的主曲率为k1、k2,则定义 ![]() 为全曲率。
为全曲率。
梅尼埃定理
设曲面曲线Γ在任意点P处的主法矢![]() 和曲面法线之夹角为θ,若对于
和曲面法线之夹角为θ,若对于![]() ·
·![]() =cosθ≠0的方向
=cosθ≠0的方向![]() ,kn=k cosθ,则表明了曲面上,任意沿
,kn=k cosθ,则表明了曲面上,任意沿![]() 方向的曲线的曲率k和沿该方向的法曲率kn的关系,称kn=k cos θ为梅尼埃(Meusnier)定理。
方向的曲线的曲率k和沿该方向的法曲率kn的关系,称kn=k cos θ为梅尼埃(Meusnier)定理。
罗德里克方程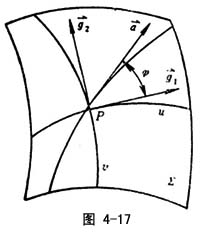 在不含有脐点的曲面上,任意点P处d
在不含有脐点的曲面上,任意点P处d![]() 、d
、d![]() 为沿着一个主方向的微分,kn表示沿这个主方向的主曲率k1或k2,则式d
为沿着一个主方向的微分,kn表示沿这个主方向的主曲率k1或k2,则式d![]() =-knd
=-knd![]() 称罗德里克(Rodriques)方程。
称罗德里克(Rodriques)方程。
欧拉公式
P为曲面Σ:![]() =
=![]() (u,v)上的一非脐点,且在P点附近,一个整片曲面内没有脐点,选择参数曲线u,v为曲率线,φ为主方向到任意切矢
(u,v)上的一非脐点,且在P点附近,一个整片曲面内没有脐点,选择参数曲线u,v为曲率线,φ为主方向到任意切矢![]() 的有向角(图4-17),则kn=k1cos2φ+k2sin2φ称欧拉(Euler)公式,它表明了任意方向
的有向角(图4-17),则kn=k1cos2φ+k2sin2φ称欧拉(Euler)公式,它表明了任意方向![]() 的法曲率kn和两个主曲率之间的关系。
的法曲率kn和两个主曲率之间的关系。
相对渐近方向
曲面Σ(1)、Σ(2)在P点相切触,在P点处相对法曲率等于零的方向,称相对渐近方向。
相对曲率
对于“有向平面”上的“有向曲率”引进的曲率概念称相对曲率。
 相对主曲率
相对主曲率
设曲面Σ(1)、Σ(2)在P点相切触。在P点处相对法曲率的最大和最小值称相对主曲率。其值kn1(12),kn2(12)=H(12)±R(12)。
相对主方向
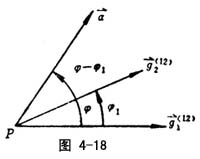
设曲面Σ(1)、Σ(2)在P点相切触,在P点处相对主曲率所在的方向 ![]() 1(12),
1(12), ![]() 2(12)(图4-18)称相对主方向。两相对主方向相互垂直
2(12)(图4-18)称相对主方向。两相对主方向相互垂直 ![]() 1(12)⊥
1(12)⊥![]() 2(12)。且-R(1)sin2a+R(2)sin2(φ-φ1)=0。
2(12)。且-R(1)sin2a+R(2)sin2(φ-φ1)=0。
相对中曲率
给定条件与“相对法曲率”相同,定义:H(12)=H(1)-H(2)为相对中曲率,它等于任意两个相互垂直方向的相对曲率的平均值。
 相对全曲率
相对全曲率
设曲面Σ(1)、Σ(2)在P点相切触,定义:在切触点P处相对主曲率k1(12)、k2(12)之积称曲面Σ(1)、Σ(2)在切触点P处的相对全曲率。K(12)=k1(12)·k2(12)=H(12)-R(12)。
相对法曲率
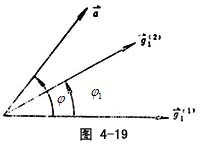
设曲面Σ(1)、Σ(2)在P点相切触,有相同的单位法矢,任意方向![]() 的法曲率分别为kn(1)、kn(2),定义:kn(12)= kn(1)-kn(2)为相对法曲率。如图(4-19)所示,φ1、φ分别为
的法曲率分别为kn(1)、kn(2),定义:kn(12)= kn(1)-kn(2)为相对法曲率。如图(4-19)所示,φ1、φ分别为 ![]() 1(1)与
1(1)与![]() 1(2)、
1(2)、![]() 1(1)与
1(1)与![]() 的有向角,于是有:
的有向角,于是有:
kn(12)=H(12)+R(1)cos2φ-R(2)cos(φ-φ1)
式中,R(1)、R(2)分别为曲面Σ(1)、Σ(2)在P点处的曲挠圆半径。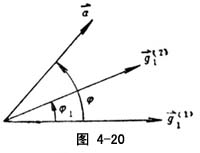 相对短程挠率
相对短程挠率
曲面Σ(1)、Σ(2)在P点处相切触,有相同的法矢![]() ,、τg(2)分别为两曲面的短程挠率(见图4-20),定义:τg(12)=τg(1)-τg(2)为相对短程挠率。于是τg(12)=-R(1)sin2φ+R(2)sin2(φ-φ1)。R(1)、R(2)为曲挠圆半径。
,、τg(2)分别为两曲面的短程挠率(见图4-20),定义:τg(12)=τg(1)-τg(2)为相对短程挠率。于是τg(12)=-R(1)sin2φ+R(2)sin2(φ-φ1)。R(1)、R(2)为曲挠圆半径。
贝特朗公式
在曲面Σ上的P点处,![]() 1和
1和![]() 的夹角为φ,τg=(k2-k1)sinφcosφ称贝特朗(Bertrand)公式。它表示了主曲率(k1,k2)和短程挠率τg之关系。若
的夹角为φ,τg=(k2-k1)sinφcosφ称贝特朗(Bertrand)公式。它表示了主曲率(k1,k2)和短程挠率τg之关系。若![]() 是主方向,则τg=0。
是主方向,则τg=0。
短程线
曲面Σ上短程曲率恒等于零的曲线Γ称短程线。曲面Σ上的曲线成为短程线的充要条件是,曲线上的主法线处处和曲面法线重合,即:![]() ·
·![]() =0,
=0,![]() =±
=±![]() 。
。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底