直角坐标系(坐标系)
在三维空间中,任选一点o,过o点做三条相互垂直的直线ox、oy、oz(这三条直线正方向上的单位矢量分别用( ![]() 、
、![]() 、
、 ![]() 表示)(图4-1),则构成直角坐标系,通称坐标系。点o称坐标系原点;ox、oy、oz为坐标轴;(
表示)(图4-1),则构成直角坐标系,通称坐标系。点o称坐标系原点;ox、oy、oz为坐标轴;(![]() 、
、![]() 、
、![]() )为底矢。直角坐标系通常记作σ=[o;x,y,z]或记作σ=[o;
)为底矢。直角坐标系通常记作σ=[o;x,y,z]或记作σ=[o;![]() 、
、![]() 、
、![]() ]。
]。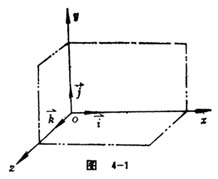
一般直角坐标系分为右手系和左手系两种类型。右手坐标系的特征是:逆时针方向旋转,当平面xoy绕oz轴逆时针方向转90°时,ox轴就代换了oy轴,其余依此类推。在左手坐标系中,可以发生同样情况,只不过是沿顺时针方向旋转而已。
基础坐标系
和固定空间相固连的直角坐标系,称基础坐标系。亦称静坐标系。记作σ=[o;![]() ,
,![]() ,
,![]() ],或σ=[o;
],或σ=[o;![]() ,
,![]() ,
,![]() ]。
]。
动坐标系
和运动物体固连在一起的坐标系,坐标系随物体的运动而运动,其位置是时间t的函数,这样的坐标系称动坐标系。和运动物体i固连的坐标系记作σ(i)=[oi;xi,yi,zi]或记作σ(i)=[oi;![]() i,
i,![]() i,
i,![]() i]。
i]。
坐标变换
空间一点P的位置原用坐标系σ(i)的参数表示,在齿轮啮合原理中,往往需要用与坐标系σ(i)有关的另一坐标系σ(j)内的参数表示,这种转换关系称坐标变换。这时称σ(i)为旧坐标系,σ(j)为新坐标系。
系数矩阵
空间P点在坐标系σ(i)中的径矢为![]() (i),改为用坐标系σ(j)内的径矢
(i),改为用坐标系σ(j)内的径矢![]() (j)表示,这种变换关系为:
(j)表示,这种变换关系为:![]() (j)=[A]
(j)=[A]![]() (i) (
(i) (![]() (i)=[A]-1
(i)=[A]-1![]() (j)) 。称[A]为系数矩阵。σ(i)为旧坐标系,σ(j)为新坐标系,若旧坐标系原点oi,在新坐标系中的位置为oi(a,b,c),这时系数矩阵[A]可写成:
(j)) 。称[A]为系数矩阵。σ(i)为旧坐标系,σ(j)为新坐标系,若旧坐标系原点oi,在新坐标系中的位置为oi(a,b,c),这时系数矩阵[A]可写成:

当oi,oj两原点重合时a=b=c=o,变成了三阶系数矩阵(虚线框内形式)。矢量变换、速度变换、底矢变换、法矢变换等都可用三阶系数矩阵;四阶系数矩阵,仅用于新旧坐标系原点不相重合的情况。
三阶基本系数矩阵
新旧坐标系原点重合,且相对绕一坐标轴转过角度φ时,两坐标系之间变换关系中的系数矩阵称基本系数矩阵。这种情况仅用于三阶系数矩阵,分下列几种情况:
图4-2a所示oj、oi重合,xj、xi重合,绕x轴转过φ角时:由σ(i)→σ(j),由σ(j)→σ(i)的系数矩阵分别为[A]xji和[A]xij
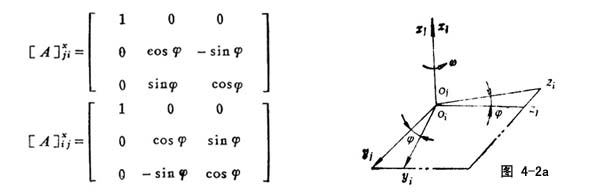
图4-2b所示oj、oi重合,yi、yj重合,绕y轴转过φ角时,由σ(i)→σ(j),σ(j)→σ(i)的系数矩阵分别为[A]yji和[A]yij
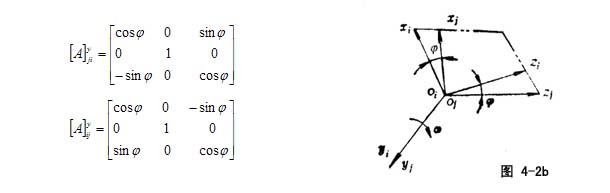
图4-2c所示oj、oi重合,zj、zi重合,绕z轴转过φ角时,由σ(i)→σ(j),σ(j)→σ(i)的系数矩阵分别为[A]zji和[A]zij
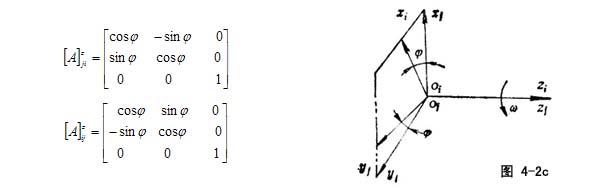
四阶基本系数矩阵
新、旧坐标系,原点不重合,且绕一坐标轴线相对转动φ角时,两坐标系变换关系中的系数矩阵,称基本系数矩阵。旧坐标系原点在新坐标系中的位置见图4-3所示。有下列情况:
图4-3a所示,xj、xi平行且绕xi转过角φ,这时σ(i)→σ(j),σ(j)→σ(i)的系数矩阵为[A]xji和[A]xij
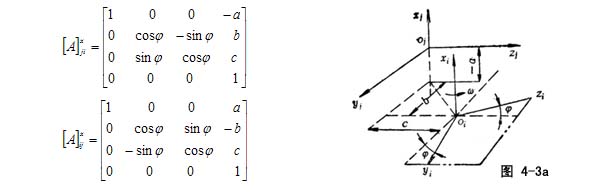
图4-3b所示,yj、yi平行且绕yi转过角φ,这时σ(i)→σ(j),σ(j)→σ(i)的系数矩阵为[A]yji和[A]yij

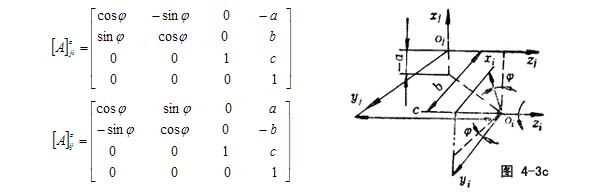
图4-3c所示,zj、zi平行,且绕z轴转过角φ,σ(i)→σ(j),σ(j)→σ(i)的系数矩阵为[A]zji和[A]zij
多次坐标变换
空间一点P由坐标系σ(i)经过坐标系σ(j)、σ(k)…变换到坐标系σ(n),这时![]() (i)、
(i)、![]() (n)的关系式可写成
(n)的关系式可写成![]() (i)p=[A]nm…[A]kj[A]ji
(i)p=[A]nm…[A]kj[A]ji![]() (i)p,式中[A]分别为坐标变换系数矩阵,若各系数矩阵之积用系数矩阵[A]ni表示,则
(i)p,式中[A]分别为坐标变换系数矩阵,若各系数矩阵之积用系数矩阵[A]ni表示,则![]() (i)、
(i)、![]() (n)之间坐标变换式可写成
(n)之间坐标变换式可写成
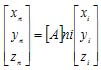

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底