椭圆是圆锥曲线的内容之一。它的定义是:到两个定点的距离和等于一个常数的2倍,这些点组成的图形就是椭圆。这个定义是非常通俗的大白话,不知道您能否读懂,不懂可以看我下面这个例图。
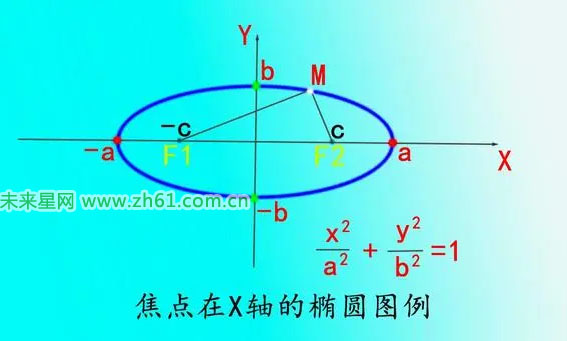
焦点在X轴椭圆图例
看上图|F1M|+|F2M|=2a(a>0),其中M点是椭圆上任意一点,a是一个大于零的定值,满足上面条件M动点围成的图形就是椭圆。这里的a是椭圆的长半轴的长度,b是椭圆短半轴的长度,c是椭圆焦点到坐标原心的长度。
椭圆方程如上图所示,它为X平方比a的平方加上y的平方比b的平方等于1,这个就是椭圆的方程表达形式,其中(-a<=x<=a,-b<=y<=b,a>0,b>0)。
椭圆离心率
椭圆离心率是椭圆的一个重要指标,它是椭圆扁平程度的一种度量,因为a>c,所以e一定是小于1大于0。e越接近1,说明椭圆越扁,e越接近0,说明椭圆越接近于圆。
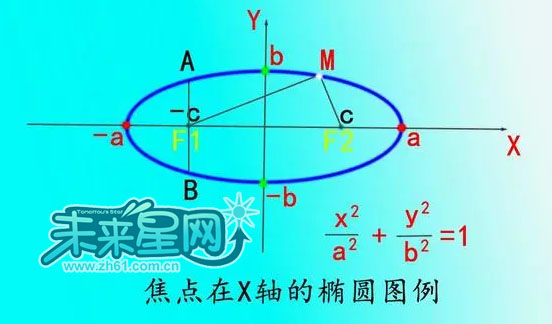
通径图例
通径也是椭圆的指标之一,如上图,A于B是椭圆上的点,AB垂直F1F2,AB并过椭圆焦点F1,我们称之AB为椭圆的通径,AB大小等于a分之2b的平方。
标准椭圆对称轴是X,Y轴,这也是椭圆的重要性质之一。
以上是本作者对于椭圆的重要内容的总结,希望能够对于读者有所帮助,如果对我的总结感到对您有帮助,欢迎点赞及加关注!下次遇到难题不迷路。

 更多
更多

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底