牛顿环干涉简介

研究光的干涉现象可以进一步加深对光的波动性的认识，产生光的干涉的仪器很多，牛顿环仪是一种常见的观察光的干涉的光学器件，用牛顿环仪可以观察到光的等厚千涉，对其干涉条纹有关量进行测量，便可以很精确地测得产生牛顿环干涉条纹的光学元器件的一些特性参数，如用牛顿环仪可以测单色光的波长、组成牛顿环仪的平凸透镜的曲率半径，检验物体表面的光洁度和平面度。用牛顿环干涉实验中测平凸透镜的曲率半径是大学物理实验中的基本实验。

牛顿环干涉实验步骤

1、准备好仪器，了解仪器的使用方法。

2、取下读数显微镜目镜帽。打开钠灯，如图摆放。

3、如图放好牛顿环，光源对准目镜筒上45°平板玻璃。

4、调节显微镜，直到看到清晰的物相。

5、清晰物相如图。

从第15环开始逐环测量定位置至第五环，再越过环心，从另一侧第5环侧至第15环为止，计算10个环的直径d。

6、对实验数据进行整理。

牛顿环实验中的误差分析

首先，在关系式：

的推导过程中，就存在两点系统误差。

然后，在实验操作中，中心不可能是点接触又是一个系统误差。

一、把观察到的干涉产生的暗环的半径当成是光线进入透镜反射点的半径。分析光路图知道，它们是不相等的。这一因素影响不大，在分析误差时常常忽略而忘记考虑。

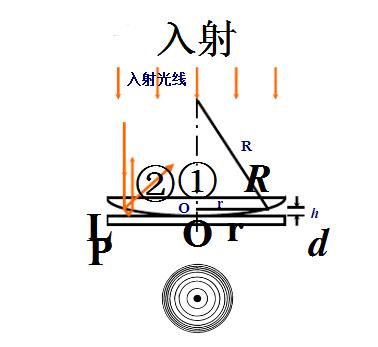
这样测出的半径比光线反射处的半径要小，由

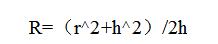
知，这一因素使得测量结果偏小。

二、推导时，忽略了h^2，这样也使得测量结果偏小。这一因素的影响也不大。

三、在实验操作中，由于中心不可能达到点接触，在重力和螺钉压力下，透镜会变形，中心会形成暗斑，造成测量结果偏差。

我们推导的公式中，用两个级次的差值进行处理，但是这样也只能避免确定暗环级次的问题，而不能真正彻底消除中心暗斑大小对结果的影响。

因为中心暗斑大小反映了透镜形变的大小，透镜受到螺钉的压力和重力，不仅是中心处发生形变，整个曲面都要形变。越靠外的地方形变越大，则Δ h变小，因此关系式中分母上的（m-n）与没有形变时已经不同了，而是变小了，可以推知，测量结果偏大了。实验书上的公式暗含着这样的近似：认为只有中心处变平，而未考虑透镜曲面上其它地方的形变。事实上，当透镜发生形变后，就不再是球面了，也不严格满足关系式：

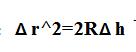
也就是说，相同的半径R处对应的空气层厚度h减小，且越靠外减小得越甚，Δ h变小，m-n变小，测量结果偏大。这个因素是影响最大的一个因素，中心暗斑越大，测量结果越不准确，越偏大。

对于这一因素，有一篇题为《牛顿环中暗斑大小对测量结果的影响》的小论文进行了探讨。

其中给出的解决方法是：

在不同的中心暗斑大小情况下分别进行测量，并记录中心暗斑的大小，然后与标准值比较观察误差大小。最后在计算机上用软件Matlab对结果进行拟合，曲率半径为纵轴，中心暗斑半径为横轴。然后就可以得到对应于中心暗斑半径为0的曲率半径值。

这样做结果的确比较准确，但是论文中也犯了一个走极端的错误，那就是，即使在理想的点接触情况下，中心暗斑的半径也不是0。

因为我们在做任何干涉实验中观察到的条纹都不是一条线，而是有粗细的。对于单色性较好的光来说，条纹的粗细主要是由于光强极值不可能比附近的光强有明显的突变造成的。如下图：

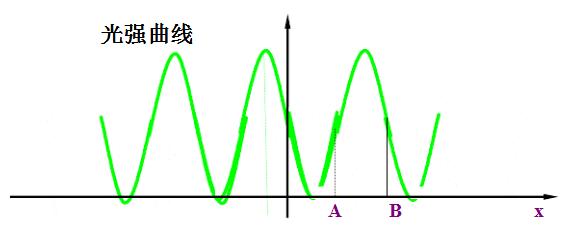
在图中A点和B点处，光强变化最快，人眼最敏感，因此A点和B点的位置是明条纹与暗条纹的分界线。从A点到B点的长度是我们看到的条纹的宽度。

因此，即使在理想的点接触条件下，中心暗斑的半径也不是0，而是有一定的大小，它比第一暗环的宽度稍大一点。中心暗斑在这个大小的时候得到的结果是相对来说最准确的。

测量结果的准确度与所用透镜的曲率半径大小也有关，曲率半径小的测得的结果更准确些。这点不难分析，因为曲率半径小的透镜发生的相对形变小，同一半径对应的空气层厚度变化小，因此测量结果的相对误差就小一些，并且曲率半径本身就小，则绝对误差更小。曲率半径大的则相反。也就是说，透镜的形变因透镜本身而异，造成的结果偏差也与透镜本身曲率半径的大小有关。我们测量出来的曲率半径，实际上是把形变后的曲面还当作球面，按照我们推导的球面情况下的公式处理求出的曲率半径。

我们如果用另一种牛顿环仪（只是笔者构想出来的模型），平衡掉重力，则可以使中心尽可能接近点接触状态。如下图：

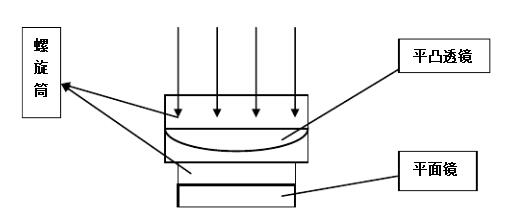
这样的牛顿环仪有很多优点：

（1） 可以抵消掉重力作用，细心调整，可以很接近点接触；

（2） 仪器筒状，不易进灰尘；

（3） 透镜四周受力，受力均匀，不易损坏。

（4） 透镜与平面镜的平行性在生产时确定，不必再进行调节，因此做实验时也省时省力。

这种牛顿环仪模型唯一的缺点可能是造价将会比较高。不过，关于透镜与平面镜的平行性，生产时也不必太严格，因为我们做实验时，用螺钉式牛顿环仪也不会把平行性调节得很好，但是现象已经很明显，因此也可以造得便宜很多。并且，几乎不用担心损坏问题，因为这种结构不易损坏。

牛顿环实验是一个重要的干涉实验，其中存在非常多的误差因素，我们做这个实验大概是为了更多地了解方法，至于精确测量透镜的曲率半径有更精确的方法。

对于用牛顿环法测量曲率半径的实验，在有限的条件下要测量出更精确的结果，就要从测量方法和误差分析上入手了。

前面分析的前两个系统误差都使得测量结果偏小，而第三个误差却使得测量结果偏大，这就造成一种巧合的存在：中心暗斑稍大却测出了比理想无形变时更接近真实值的结果。也是我们做这个实验时既能测出偏小结果又能测出偏大结果的重要原因。