前面已经讲解了空间和时间反演对称性，为了故事的完整性，再简单讨论一下平移对称性，以及这种对称性会产生什么样的物理结果。

一、空间平移对称性--Bloch theorem  对应动量守恒

固体物理中最重要的结论之一，就是布洛赫定理，它是空间平移对称性的必然结果: 波函数等于一个相因子和一个周期性函数的乘积，其本身不是一个周期性函数，其证明可见各类教科书，关于群论的一个简单证明可翻阅之前的推送。这里重点看一下时间平移对称性。

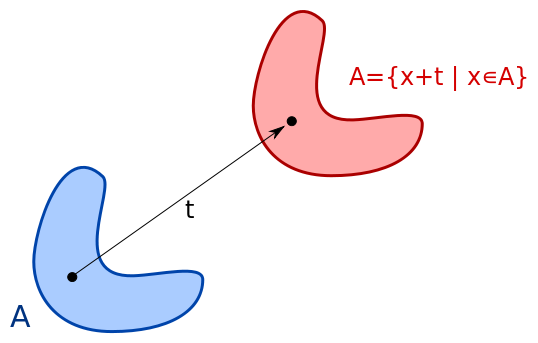
空间平移对称性 Symmetry of space translation 物理规律并不依赖于空间坐标原点的选择，将整个空间平移一个位置，物理规律不会改变。

中文名:空间平移对称性
外文名:Symmetry of space translation
如果在中国的实验室里做了某个实验，得到了某个物理结果，那么在美国的实验室里在完全相同的条件下做同一实验，必然会得到同样的结果，这种对称性称为物理规律的空间平移不变性或空间平移对称性，或者说，具有空间均匀性。

二、时间平移对称性--Floquet theorem

其实就是Bloch theorem在时间坐标上的推广，哈密顿量是时间的周期函数，它们的对比如下

时间平移对称  能量守恒

时间平移对称意味着在时间演化下哈密顿量不变, 而哈密顿量就是能量, 因此时间演化下能量不变, 即能量守恒.

三、Time dependent Schroedinger equation

这时哈密顿量是time dependent的，但我们可以通过傅里叶变换将其转换成等效的time independent的问题

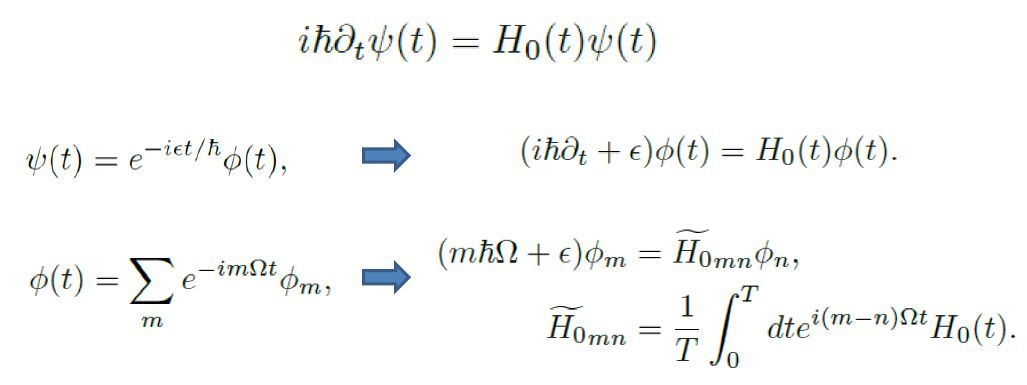
关于Floquet理论的细节和应用以后应该会讲。。。

Ref:

1. Jon H. Shirley. Phys. Rev. 138, B979