带电粒子在匀强磁场中的运动是物理常见题，在这篇文章中，我们把一些关键的物理量及解题思路做一个梳理。

关键物理量梳理

洛伦兹力

当电荷速度方向与磁场方向垂直时，洛伦兹力的大小f=Bvq；当电荷运动方向与磁场方向夹角为θ时，洛伦兹力的大小f=Bvqsinθ；不难看出，洛伦兹力最大的特点就是大小与速度有关。

磁场对静止的电荷无作用力，磁场只对运动电荷有作用力，这与电场对其中的静止电荷或运动电荷总有电场力的作用是不同的。

洛伦兹力的方向始终与运动的速度方向垂直，可通过左手定则来判定。

带电粒子在洛伦兹力的作用下（充当向心力），可以做匀速率圆周运动。

荷质比

带电粒子的电荷量和其质量的比值叫荷质比，即k=q/m。对某种固定的粒子，其荷质比是常量。例如，电子的比荷为e/me=1.758×10^11C/kg。

偏转半径

带电粒子在匀强磁场中的运动，在只有洛伦兹力作用下，粒子做圆周偏转，其半径公式为：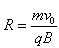

由此可见，粒子的半径仅与荷质比、速度、磁场大小相关。

偏转角

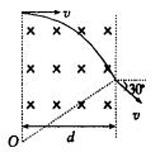
粒子在偏转中，与原始速度矢量间夹角称之为偏转角。如下图所示，经历了一段圆弧的偏转后，粒子的偏转角为30°；

需要注意的是，粒子偏转角等于其偏转弧所对应的圆心角。这是初中几何中讲过的弦切角定理。

周期

带电粒子在匀强磁场中的运动，在只有洛伦兹力作用下，粒子做圆周偏转，其周期公式为：

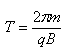
解题思路梳理

带电粒子在匀强磁场中的运动类问题通用解题步骤

（1）明确轨迹。

带电粒子运动为圆周运动，需要同学们首先确定好运动轨迹。有些题是没有明确告诉你轨迹的，需要你自己分析，自己去画图（草图），有时候画出来图还要接着修改。

（2）找圆心。

确定了大致的运动轨迹，就开始研究圆心。圆心一般是两个点的速度的垂线交点。

（3）构建合适的三角形。

结合题意条件，构建一个直角三角形，并在其中表述偏转半径R；一般要用到很多几何知识。

（4）结合偏转半径的物理公式进行求解。

有了半径R之后，结合上述物理公式R=mv/Bq；就可以求解出来你需要的物理量了。

解题中三个物理量的确定

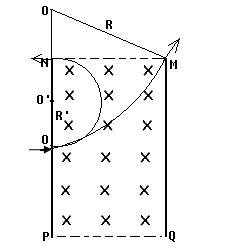
⒈圆心的确定

圆心一定在与速度方向垂直的直线上，根据入射点和出射点的速度方向做出垂线，交点即为圆心。

⒉半径的计算

一般是利用几何知识解直角三角形。

⒊带电粒子在有界磁场中运动时间的确定

利用圆心角和弦切角的关系或四边形内角和等于360度或速度的偏向角（带电粒子射出磁场的速度方向与射入磁场的速度方向之间的夹角）等于圆弧轨道所对的圆心角，再由公式t/T=θ/360来求运动时间。

找圆心、画轨迹是解题的基础

带电粒子垂直于磁场进入一匀强磁场后在洛伦兹力作用下必作匀速圆周运动，抓住运动中的任两点处的速度，分别作出各速度的垂线，则二垂线的交点必为圆心；或者用垂径定理及一处速度的垂线也可找出圆心；再利用数学知识求出圆周运动的半径及粒子经过的圆心角从而解答物理问题。

导致轨道半径变化的原因归纳

①带电粒子速度变化导致半径变化。如带电粒子穿过极板速度变化；带电粒子使空气电离导致速度变化；回旋加速器加速带电粒子等。

②磁场变化导致半径变化。如通电导线周围磁场，不同区域的匀强磁场不同；磁场随时间变化。

③动量变化导致半径变化。如粒子裂变，或者与别的粒子碰撞；

④电量变化导致半径变化。如吸收电荷等。总之，由看m、v、q、B中某个量或某两个量的乘积或比值的变化就会导致带电粒子的轨道半径变化。

临界问题解题思路

带电粒子在磁场中运动的临界问题的原因有：粒子运动范围的空间临界问题；磁场所占据范围的空间临界问题，运动电荷相遇的时空临界问题等。审题时应注意恰好，最大、最多、至少等关键字。

寻找产生极值的条件的常用思路梳理：

①直径是圆的最大弦；

②同一圆中大弦对应大的圆心角；

③由轨迹确定半径的极值。