德布罗意公式揭示了物质粒子具有波动性质的本质,为研究粒子行为提供新视角。公式λ=h/p表示物质波波长与动量关系,对量子力学发展有深远影响。实验验证了德布罗意公式的预测,证实了微观粒子的波动性质。德布罗意公式揭示波粒二象性的统一,对现实世界本质的观念提出了挑战。
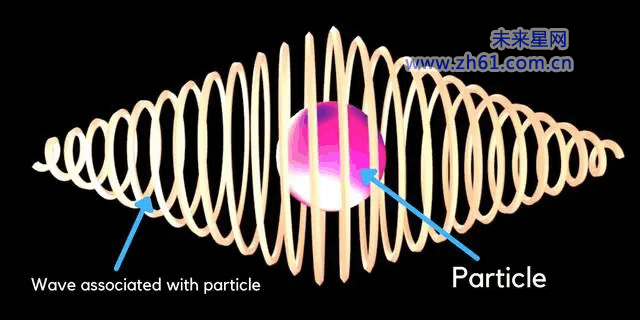
德布罗意波的概念展示了微观粒子具有波粒二象性,即粒子同时表现出波动性质和粒子性质。这种波粒二象性意味着微观粒子既具有波动性(如光波)的特征,也具有粒子性(如物质粒子)的特征。德布罗意公式λ=h/p(其中λ是波长,h是普朗克常数,p是动量)具体说明了粒子波动性质的程度,即粒子的动量越小,其对应的德布罗意波长越长,波动性质越明显;反之,粒子的动量越大,德布罗依波长越短,粒子性质越显著。
德布罗意波的概念不仅在理论上具有重要意义,也在实验中得到了验证。例如,电子衍射实验成功地证实了电子的波动性质。此外,不确定性原理(ΔxΔp≥h/4π)进一步揭示了微观粒子波动性质和粒子性质之间的基本联系。
德布罗意公式是量子力学中的一项重要成就,它揭示了物质粒子具有波动性质的本质。这一公式由法国物理学家路易斯·德布罗意在1924年提出,为研究粒子行为提供了一种全新的视角。本文将深入探讨德布罗意公式的物理背景、推导过程以及其带来的重要意义,帮助读者更好地理解波粒二象性的奇妙统一。
一、物质波的概念
在经典物理学中,我们习惯将光看作是波动的电磁辐射,而将物质视为粒子。然而,实验观察到的现象却难以用粒子模型完全解释,例如电子的干涉和衍射现象。为了解释这些奇妙的实验结果,德布罗意提出了物质波的概念。他认为,与光波类似,物质粒子也具有波动性质,其波长与动量之间存在一种关系。
二、德布罗意公式的推导
德布罗意通过对光波和物质粒子性质的比较,提出了物质波的波长与动量之间的关系,即德布罗意公式:
λ = h / p
其中,λ表示物质波的波长,h为普朗克常数(Planck constant),p为粒子的动量。这一公式揭示了波动性与粒子动力学性质之间的联系。
推导德布罗意公式的一个关键思路是将粒子视为波动波包的叠加。通过数学分析,可以证明波包的波矢(k)与物质粒子的动量(p)之间存在线性关系,即k = p / ħ,其中ħ为约化普朗克常数。根据波动的基本性质,波矢与波长之间存在反比关系,即k = 2π / λ。将这两个关系结合起来,就得到了德布罗意公式。
三、德布罗意公式的意义和实验验证
德布罗意公式的提出对量子力学的发展有着深远的影响。它揭示了微观粒子的波动性质,为解释和预测实验现象提供了全新的工具。通过德布罗意公式,我们可以计算物质波的波长,从而预测粒子的行为,如干涉、衍射和散射等。
实验上,德布罗意公式的预测已经得到了广泛的验证。例如,电子的干涉实验观察到了电子的波动性质,与德布罗意公式的预测相符。同样地,中子、原子、分子等微观粒子的干涉和衍射实验也进一步证实了德布罗意公式的有效性。
四、波粒二象性的统一
德布罗意公式的提出揭示了波动性和粒子性在微观尺度上的统一。在传统的物理学观念中,波动和粒子性被视为两种截然不同的性质,但德布罗意公式的推导和实验验证表明,物质粒子既可以表现出粒子的局域性质,又可以展现出波动的全局性质。
这种波粒二象性的统一在量子力学中起着关键作用。它不仅解释了微观世界中的各种奇特现象,如干涉、衍射和量子隧穿等,还为粒子的波函数描述提供了理论基础。在波函数的框架下,我们可以用概率的方式描述粒子的存在和行为,而波函数的演化则受到著名的薛定谔方程控制。
波粒二象性的统一也引发了哲学上的深思。它挑战了我们对物质本质的传统观念,使我们不得不重新审视世界的本质和我们对现实的认识方式。德布罗意公式的提出为量子力学奠定了基础,开启了一扇通往微观世界的新大门,带领我们进入了一个全新的物理学领域。

 更多
更多
 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底