史瓦西半径是任何具有质量的物质都存在的一个临界半径特征值。在物理学和天文学中,尤其在万有引力理论、广义相对论中它是一个非常重要的概念。1916年卡尔·史瓦西首次发现了史瓦西半径的存在,他发现这个半径是一个球状对称、不自转的物体的重力场的精确解。 一个物体的史瓦西半径与其质量成正比。太阳的史瓦西半径约为3千米,地球的史瓦西半径只有约9毫米。
中文名:史瓦西半径
外文名:Schwarzschild radius
发现者:卡尔·史瓦西
发现时间:1916年
黑洞
物体的实际半径小于其史瓦西半径的物体被称为黑洞。在不自转的黑洞上,史瓦西半径所形成的球面组成一个视界(仅对于不自转的黑洞,自转的黑洞的情况稍许不同)。光和粒子均无法逃离这个球面。银河中心的超大质量黑洞的史瓦西半径约为780万千米。史瓦西半径不是黑洞实体半径。黑洞的半径不能直接用肉眼看,肉眼看到的是史瓦西半径。
半径公式
史瓦西半径(Schwarzschild radius)的公式,其实是从物体逃逸速度的公式衍生而来。该值的含义是,如果特定质量的物质被压缩到该半径值之内,将没有任何已知类型的力可以阻止该物质在自身引力的条件下将自己压缩成一个黑洞。
它将物体的逃逸速度设为光速,配合万有引力常数及天体质量,便能得出其史瓦西半径。
根据天体逃逸速度(v)的计算公式计算天体的史瓦西半径。
v指天体的逃逸速度,G为万有引力常数,M为天体质量,R为天体质心与被吸引物体质心的距离。物体的速度若小于一个天体的逃逸速度,就不能摆脱其引力束缚,会被该天体吸引,无法脱离轨道而逃逸到星际空间。

 更多
更多
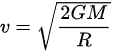

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底